Question

【题目】已知⊙O的半径为3，△ABC内接于⊙O，AB=3 ，AC=3 ，D是⊙O上一点，且AD=3，则CD的长应是（ ）
A.3
B.6
C.
D.3或6

Answer 1

【答案】D
【解析】解：第一种情况，当点D在AC弧上时，连接OA、OC、OD．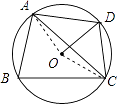
所以AD=OA=OC=OD=3，△AOD是等边三角形，∠ADO=∠DAO=∠AOD=60°．
过O作OP垂直弦AC于P，根据垂径定理，PA=PC= AC= ．
∴在Rt△AOP中，OP= ，
∴∠OAP=30°，∠AOP=60°=∠AOD．
∴OP与OD重合，即OD垂直平分弦AC，所以CD=AD=3．
第二种情况：当点D在AB弧上时，同理得△AOD是等边三角形，∠AOD=60°．
由（1）知∠AOC=120°．
∴∠AOD+∠AOC=180°，即D、O、C在同一直线上，故CD=6．
故选D．
【考点精析】利用勾股定理的概念和垂径定理对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．