
 如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠AEB=60°,AB=AD=2cm,则梯形ABCD的周长为10cm.
如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠AEB=60°,AB=AD=2cm,则梯形ABCD的周长为10cm. 分析 先根据等腰梯形ABCD中,AD∥BC,AE∥DC得出四边形AECD是平行四边形,故AE=CD,AD=CE,再由AB=CD可知AB=AE,由∠AEB=60°可知△ABE是等边三角形,故AB=AE=BE=2,再由AD=AB=2即可得出结论.
解答 解:∵等腰梯形ABCD中,AD∥BC,AE∥DC,
∴四边形AECD是平行四边形,
∴AE=CD,AD=CE.
∵AB=CD,
∴AB=AE.
∵∠AEB=60°,
∴△ABE是等边三角形,
∴AB=AE=BE=2cm.
∵AD=AB=2cm,
∴BC=BE+CE=4cm,
∴梯形ABCD的周长=AB+AD+CD+BC=2+2+2+4=10(cm).
故答案为:10.
点评 本题考查的是等腰梯形的性质,熟知平行四边形及等边三角形的判定定理是解答此题的关键.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:选择题
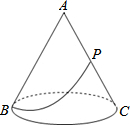 如图,有一圆锥形粮仓,其正视图为边长是4m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠,则小猫经过的最短路程为( )
如图,有一圆锥形粮仓,其正视图为边长是4m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠,则小猫经过的最短路程为( )| A. | 5m | B. | $3\sqrt{5}$m | C. | 6m | D. | $2\sqrt{5}$m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com