

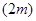 ;∠BOE=2∠COF;(2)成立;(3)16°
;∠BOE=2∠COF;(2)成立;(3)16°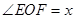 ,根据角平分线的性质可得
,根据角平分线的性质可得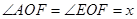 ,即可得到
,即可得到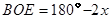 ,再由
,再由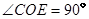 可得
可得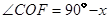 ,从而得到结论;
,从而得到结论; (∠BOE-∠BOD),即可求得结果.
(∠BOE-∠BOD),即可求得结果.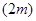 °;所以∠BOE=2∠COF;
°;所以∠BOE=2∠COF;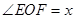
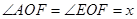
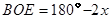
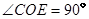
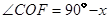
 (180°-∠BOE)=25°
(180°-∠BOE)=25°  (∠BOE-∠BOD)
(∠BOE-∠BOD) (130°-∠BOD)
(130°-∠BOD)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 等于线段
等于线段 时,小明的具体做法如下:
时,小明的具体做法如下: .
. 
 ,使得线段
,使得线段 .
. ;
; 上截取
上截取 .
. 为所求.
为所求.
 .
. 
 上作线段
上作线段 ,使得
,使得 ;(不要求写作法和结论,保留作图痕迹)
;(不要求写作法和结论,保留作图痕迹) 的中点
的中点 .若
.若 ,求线段
,求线段 的长.(要求:第(2)问重新画图解答)
的长.(要求:第(2)问重新画图解答)查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
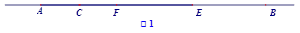
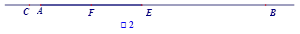
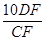 值;若不存在,请说明理由.
值;若不存在,请说明理由.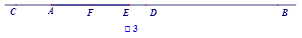
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com