
【题目】(8分)如图,在ABCD中,E、F为对角线AC上的两点,且AE=CF,连接DE、BF,
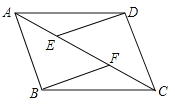
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF.
【答案】(1)△ABC≌△CDA,△ABF≌△△CDE,△ADE≌△CBF;(2)证明见试题解析.
【解析】
试题分析:(1)根据平行四边形的性质得出AB=CD,AD=CB,AB∥CD,AD∥CB,进一步得到∠BAF=∠DCE,∠DAE=∠BCF,由SSS证明△ABC≌△CDA;由SAS证明△ABF≌△CDE;由SAS证明△ADE≌△CBF(SAS);
(2)由△ABF≌△△CDE,得出∠AFB=∠CED,即可证出DE∥BF.
试题解析:(1)△ABC≌△CDA,△ABF≌△△CDE,△ADE≌△CBF;理由如下:
∵四边形ABCD是平行四边形,∴AB=CD,AD=CB,AB∥CD,AD∥CB,∴∠BAF=∠DCE,∠DAE=∠BCF,在△ABC和△CDA中,∵AB=CD,CB=AD,AC=CA,∴△ABC≌△CDA(SSS);
∵AE=CF,∴AF=CE,在△ABF和△CDE中,∵AB=CD,∠BAF=∠DCE,AF=CE,∴△ABF≌△CDE(SAS);
在△ADE和△CBF中,∵AD=CB,∠DAE=∠BCF,AE=CF,∴△ADE≌△CBF(SAS).
(2)∵△ABF≌△△CDE,∴∠AFB=∠CED,∴DE∥BF.


科目:初中数学 来源: 题型:
【题目】如图a,有两个全等的正三角形ABC和DEF,点D、C分别为△ABC、DEF的内心;固定点D,将△DEF顺时针旋转,使得DF经过点C,如图b,则图a中四边形CNDM与图b中△CDM面积的比为( ) 
A.2:1
B.2: ![]()
C.4:3
D.![]() :
: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
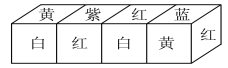
【题目】把正方体的六个面分别涂上六种不同颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
现将上述大小相同,颜色、花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问长方体的下底面共有多少朵花?
颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
花的朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王红有5张写着以下数字的卡片,请按要求抽出卡片,完成下列各题:![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最小,最小值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最大,最大值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1﹣(﹣2)]),请另写出一种符合要求的运算式子 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了该图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2016次后形成的图形中所有的正方形的面积和是( )

A. 1 B. 2015 C. 201 D. 2017
查看答案和解析>>
科目:初中数学 来源: 题型:
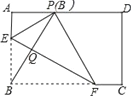
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是 。
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com