
【题目】如图a,有两个全等的正三角形ABC和DEF,点D、C分别为△ABC、DEF的内心;固定点D,将△DEF顺时针旋转,使得DF经过点C,如图b,则图a中四边形CNDM与图b中△CDM面积的比为( ) 
A.2:1
B.2: ![]()
C.4:3
D.![]() :
: ![]()
【答案】C
【解析】解:如图所示:连接MN、CD. 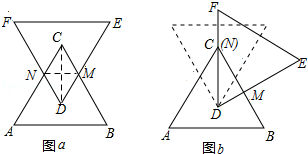
设MN的长为a,CD= ![]() a,则四边形CNDM的面积=
a,则四边形CNDM的面积= ![]() MNCD=
MNCD= ![]() ×a×
×a× ![]() a=
a= ![]() a2 ,
a2 ,
∵∠DCM=30°,∠CDM=60°,
∴DM= ![]() DC=
DC= ![]() ,CM=
,CM= ![]() a.
a.
∴△CDM= ![]() DMCM=
DMCM= ![]() ×
× ![]() ×
× ![]() =
= ![]() a2 .
a2 .
∴四边形CNDM与图b中△CDM面积的比=4:3.
故选;C.
连接MN、CD.由等三角形的性质可知∠DCM=30°,设MN的长为a,CD= ![]() a,由四边形CNDM的面积=
a,由四边形CNDM的面积= ![]() MNCD可求得四边形CNDM的面积,然后在△DCM中,依据特殊锐角三角函数值可求得DM、CM的长,依据三角形的面积公式可求得△CDM的面积,从而可求得答案.
MNCD可求得四边形CNDM的面积,然后在△DCM中,依据特殊锐角三角函数值可求得DM、CM的长,依据三角形的面积公式可求得△CDM的面积,从而可求得答案.


科目:初中数学 来源: 题型:
【题目】如图1,![]() ,
,![]() ,
,![]() ,AD、BE相交于点M,连接CM.
,AD、BE相交于点M,连接CM.![]() 求证:
求证:![]() ;
;![]() 求
求![]() 的度数
的度数![]() 用含
用含![]() 的式子表示
的式子表示![]() ;
;![]() 如图2,当
如图2,当![]() 时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断
时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断![]() 的形状,并加以证明.
的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我中华”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,则下列说法中错误的是( )
A. 甲、乙得分的平均数都是8 B. 甲得分的众数是8,乙得分的众数是9
C. 甲得分的中位数是9,乙得分的中位数是6 D. 甲得分的方差比乙得分的方差小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一小题计分.
①若单项式﹣xmyn+4 与 5x2y 是同类项,则 nm 的值为____.
②实施西部大开发战略是党中央的重大决策,我国国土面积约为960 万平方千米,而我国西部地区的面积占我国国土面积的 ![]() ,用科学记数法表示我国西部地区的面积约为_____平方千米.
,用科学记数法表示我国西部地区的面积约为_____平方千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人两次同时在一家粮店购买大米,两次大米的价格分别为每千克a元和b元(a≠b).甲每次买100千克大米,乙每次买100元大米.
(1)用含a、b的代数式表示:甲两次购买大米共需付款 元,乙两次共购买 千克大米.若甲两次购买大米的平均单价为每千克Q1元,乙两次购买大米的平均单价为每千克Q2元.则:Q1= ;Q2= .
(2)若规定谁两次购粮的平均价格低,谁购粮的方式就更合理,请你判断比较甲、乙两人的购粮方式,哪一个更合理,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三角形内有n个点,在这些点及三角形顶点之间用线段连接起来,使得这些线段互不相交,且又能把原三角形分割为不重叠的小三角形.如图:若三角形内有1个点时此时有3个小三角形;若三角形内有2个点时,此时有5个小三角形.则当三角形内有3个点时,此时有个小三角形;当三角形内有n个点时,此时有个小三角形.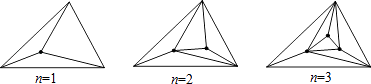
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展课外球类特色的体育活动,决定开设A:羽毛球、B:篮球、C:乒乓球、 D:足球四种球类项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.

(1)样本中最喜欢A项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生3000人,请根据样本估计全校最喜欢足球的学生人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚在课外书中看到这样一道有理数的混合运算题:
计算:![]()
她发现,这个算式反映的是前后两部分的和,而这两部分之间存在着某种关系,利用这种关系,他顺利地解答了这道题。
(1)前后两部分之间存在着什么关系?
(2)先计算哪步分比较简便?并请计算比较简便的那部分。
(3)利用(1)中的关系,直接写出另一部分的结果。
(4)根据以上分析,求出原式的结果。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在ABCD中,E、F为对角线AC上的两点,且AE=CF,连接DE、BF,
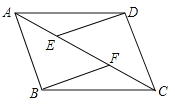
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com