
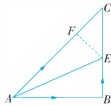
【题目】如图,在Rt△ABC的场地上,∠B=90°,AB=BC,∠CAB的平分线AE交BC于点E.甲、乙两人同时从A处出发,以相同的速度分别沿AC和A→B→E线路前进,甲的目的地为C,乙的目的地为E.请你判断一下,甲、乙两人谁先到达各自的目的地?并说明理由.
【答案】同时到达
【解析】试题分析:
由题意可知:这里是要比较AB+BE与AC的大小关系.
如图,过点E作EF⊥AC于点F,则由角平分线的性质可得BE=EF,证△EFC是等腰直角三角形可得EF=EC,从而可得BE=FC;再证△ABE≌△AFE可得AB=AF,从而可得AB+BE=AC,说明甲、乙二人会同时达到目的地.
试题解析:
甲、乙会同时到达目的地.理由如下:
过点E作EF⊥AC于点F,∵AE平分∠CAB,∠B=90°,
∴EF=EB,∠CAE=∠BAE,
∵AB=BC,∠B=90°,
∴∠C=![]() .
.
∵EF⊥AC,
∴∠EFC=90°,
∴∠CEF=90°-∠C=45°=∠C,
∴EF=CF.
∴BE=CF,
在△AEF和△AEB中, 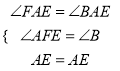 ,
,
∴△AEF≌△AEB,
∴AF=AB,
∴AB+BE=AF+CF=AC,故甲、乙同时到达目的地.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一个直角三角形ABC的直角边BC=a,AC=b,三角形内部圆的半径为r. 
(1)用含a、b、r的式子表示阴影部分面积(结果保留π);
(2)当a=10,b=6,r=2时,计算阴影部分的面积.(π取3.14,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店有2个进价不同的计算器都卖了80元,其中一个盈利60%,另一个亏本20%,在这笔买卖中,这家商店( )
A.不赔不赚
B.赚了10元
C.赔了10元
D.赚了8元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正六边形ABCDEF在直角坐标系内的位置如图所示,点A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转.若每次翻转60°,则经过2017次翻转之后,点B的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列推理过程填写完整. 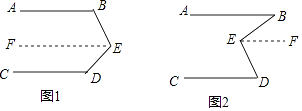
(1)如图1,已知∠B+∠BED+∠D=360°,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D+∠DEF=180°,()
∵∠B+∠BED+∠D=360°,(已知)
∴∠B+∠BEF=∠B+∠BED+∠D﹣(∠D+∠DEF)=360°﹣180°=180°
∴EF∥AB,()
∴∥ , (平行于同一直线的两直线平行)
(2)如图2,已知∠BED=∠B+∠D,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D=∠FED,()
∵∠BED=∠B+∠D(已知)
∴∠B=∠BEF﹣∠D=∠BED﹣∠FED=∠BEF,
∴∥ , ()
∴∥ . (平行于同一直线的两直线平行)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com