
【题目】将下列推理过程填写完整. 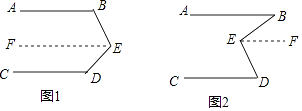
(1)如图1,已知∠B+∠BED+∠D=360°,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D+∠DEF=180°,()
∵∠B+∠BED+∠D=360°,(已知)
∴∠B+∠BEF=∠B+∠BED+∠D﹣(∠D+∠DEF)=360°﹣180°=180°
∴EF∥AB,()
∴∥ , (平行于同一直线的两直线平行)
(2)如图2,已知∠BED=∠B+∠D,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D=∠FED,()
∵∠BED=∠B+∠D(已知)
∴∠B=∠BEF﹣∠D=∠BED﹣∠FED=∠BEF,
∴∥ , ()
∴∥ . (平行于同一直线的两直线平行)
【答案】
(1)两直线平行,同旁内角互补;同旁内角互补,两直线平行;AB;CD
(2)两直线平行,内错角相等;AB;EF;内错角相等,两直线平行;AB;CD.
【解析】(1.)证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行) ∵EF∥CD,
∴∠D+∠DEF=180°,( 两直线平行,同旁内角互补 )
∵∠B+∠BED+∠D=360°,( 已知 )
∴∠B+∠BEF=∠B+∠BED+∠D﹣(∠D+∠DEF )=360°﹣180°=180°,
∴EF∥AB,( 同旁内角互补,两直线平行 )
∴AB∥CD,( 平行于同一直线的两直线平行);
所以答案是:两直线平行,同旁内角互补;同旁内角互补,两直线平行;AB;CD;
(2.)证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D=∠FED,( 两直线平行,内错角相等 )
∵∠BED=∠B+∠D,(已知)
∴∠B=∠BED﹣∠D=∠BED﹣∠FED=∠BEF,
∴AB∥EF,( 内错角相等,两直线平行 )
∴AB∥CD,( 平行于同一直线的两直线平行).
所以答案是:两直线平行,内错角相等;AB;EF;内错角相等,两直线平行;AB;CD.
【考点精析】通过灵活运用平行公理和平行线的判定,掌握平行公理――平行线的存在性与惟一性;经过直线外一点,有且只有一条直线与这条直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行即可以解答此题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】下面去括号正确的是( )
A. x2﹣(2y2﹣x+z)=x2﹣2y2﹣x+z
B. 2a+(﹣6x+4y﹣2)=2a﹣6x+4y﹣2
C. 3a﹣[6a﹣(4a﹣1)]=3a﹣6a﹣4a+1
D. ﹣(2x2﹣y)+(z+1)=﹣2x2﹣y﹣z﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按如图所示的方式摆放餐桌和椅子,用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
(3)按如图所示的方式摆放餐桌和椅子,100张餐桌可以坐多少人?
(4)按如图所示的方式摆放餐桌和椅子,能否刚好坐80人?请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
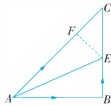
【题目】如图,在Rt△ABC的场地上,∠B=90°,AB=BC,∠CAB的平分线AE交BC于点E.甲、乙两人同时从A处出发,以相同的速度分别沿AC和A→B→E线路前进,甲的目的地为C,乙的目的地为E.请你判断一下,甲、乙两人谁先到达各自的目的地?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于A,B两点,且交y轴于点C.已知点A(1,4),点B在第三象限,且点B的横坐标为t(t<﹣1).
的图象相交于A,B两点,且交y轴于点C.已知点A(1,4),点B在第三象限,且点B的横坐标为t(t<﹣1).
(1)求反比例函数的解析式;
(2)用含t的式子表示k,b;
(3)若△AOB的面积为3,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球,13个黑球和22个红球,它们除颜色外都相同.
(1)小明和小红玩摸球游戏,规定每人摸球后再将摸到的球放回去为一次游戏.若摸到黑球小明获胜,摸到黄球小红获胜,这个游戏对双方公平吗?请说明你的理由;
(2)现在裁判想从袋中取出若干个黑球,并放入相同数量的黄球,使得这个游戏对双方公平,问取出了多少黑球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com