练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知关于x的一元二次方程x2-2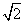x+m=0,有两个不相等的实数根.

    (1)求实数m的最大整数值；

    (2)在(1)的条件下，方程的实数根是x1，x2,求代数式x12+x22-x1x2的值.


    （1）由题意，得Δ＞0，

    即(-2)2-4m＞0，解得m＜2.

    ∴m的最大整数值为m=1.

    (2)把m=1代入关于x的一元二次方程x2-2x+m=0得x2-2x+1=0，

    根据根与系数的关系：x1+x2=2，x1x2=1，

    ∴x12+x22-x1x2=(x1+x2)2-3x1x2=(2)2-3×1=5.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知：点P(1-2a，a-2)关于原点的对称点在第一象限内，且a为整数，则关于x的分式方程

      ＝2的解是(     )

        A.5                 B.1                    C.3                     D.不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一元二次方程x2+px-2＝0的一个根为2，则p的值为(     )

    A.1              B.2                C.-1                  D.-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知关于x的一元二次方程(k-1)x2-2x+1=0有两个不相等的实数根，则k的取值范围是(     )

    A.k＜-2             B.k＜2             C.k＞2              D.k＜2且k≠1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


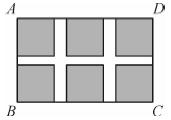
    如图，某小区规划在一个长30 m、宽20 m的长方形ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分种花草.要使每一块花草的面积都为78 m2，那么通道的宽应设计成多少m？设通道的宽为x m，由题意列得方程          .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0，其中a、b、c分别为△ABC的三边的长.

    (1)如果x=-1是方程的根，试判断△ABC的形状，并说明理由；

    (2)如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；

    (3)如果△ABC是等边三角形，试求这个一元二次方程的根.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图是我市几个旅游景点的大致位置示意图，如果用(0，0)表示新宁崀山的位置，用(1，5)表示隆回花瑶的位置，那么城步南山的位置可以表示为(     )

      A.(2，1)        B.(0，1)        C.(-2，-1)         D.(-2，1)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小明从家出发，外出散步，到一个公共阅报栏前看了一会儿报后，继续散步了一段时间，然后回家.如图描述了小明在散步过程中离家的距离s(米)与散步所用的时间t(分)之间的函数关系.根据图象，下列信息错误的是(     )

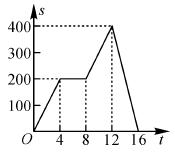
      A.小明看报用时8分钟

      B.公共阅报栏距小明家200米

      C.小明离家最远的距离为400米

      D.小明从出发到回家共用时16分钟

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    “五一节”期间，王老师一家自驾游去了离家170千米的某地，下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象，当他们离目的地还有20千米时，汽车一共行驶的时间是(     )

      A.2小时              B.2.2小时             C.2.25小时          D.2.4小时

    查看答案和解析>>

    同步练习册答案