
【题目】如图,点A是反比例函数y=![]() (m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
(m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图像及y轴分别交于B、
D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.

【答案】(1) B(2n,![]() );(2)证明见解析;(3)y=x+6.
);(2)证明见解析;(3)y=x+6.
【解析】
试题(1)由题意可表示出点A的坐标,根据BD是AC的中垂线可得点B的纵坐标,代入反比例函数解析式即可求得横坐标;
(2)先根据AM=CM、BM=MD证明四边形ABCD是平行四边形,再根据BD⊥AC即可证明四边形ABCD是菱形;
(3)根据题意求得点A、B的坐标即可得.
试题解析:(1)当x=n时,y=![]() ,∴A(n,
,∴A(n,![]() ),
),
由题意知BD是AC的中垂线,∴点B的纵坐标为![]() ,
,
∴把y=![]() 代入y=
代入y=![]() 得x=2n,∴B(2n,
得x=2n,∴B(2n,![]() );
);
(2)由(1)可知AM=CM,BM=MD=![]() ,
,
∴四边形ABCD是平行四边形,
又∵BD⊥AC,∴平行四边形ABCD是菱形;
(3)当四边形ABCD是正方形时,△ABM为等腰直角三角形,
∵△ABM的面积为2,∴AM=BM=2,∴A(-2,4),B(-4,2),
由此可得直线AB所对应的函数表达式为y=x+6.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )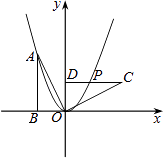
A.( ![]() ,
, ![]() )
)
B.(2,2)
C.( ![]() ,2)
,2)
D.(2, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)直接写出点A1,B1,C1的坐标.
A1 , B1 , C1 ;
(3)请你求出△A1B1C1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB是⊙O的直径,C为⊙O上一点,AD垂直于经过点C的直线DE,垂足为点D,AC平分∠DAB.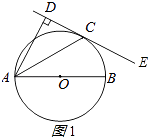
(1)求证:直线DE是⊙O的切线;
(2)连接BC,猜想:∠ECB与∠CAB的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC内接于⊙O,点D在OC的延长线上,sinB= ![]() ,∠CAD=30°.
,∠CAD=30°.
(1)求证:AD是⊙O的切线;
(2)若OD⊥AB,BC=5,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com