解:(1)证明:∵△ABC与△BDE都是等边三角形,
∴∠A=∠C=∠BDE=60°,
∵∠ADF+∠BDE=∠C+∠DBC,
∴∠ADF=∠DBC,
∴△BCD∽△DAF.
(2)①解:∵△BCD∽△DAF,
∴
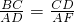
,
∵BC=1,设CD=x,AF=y,
∴
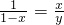
,
∴y=x-x
2(0<x<1).
②解:解法一:∵△ABC与△BDE都是等边三角形,
∴∠E=∠C=60°,∠EBD=∠CBA=60°,
∴∠EBF=∠CBD,
∴△EBF∽△CBD,
∴

,
∴BE•BD=BF•BC
∵BE=BD,
∴BE
2=BF•BC,
BC=1,
∴BE
2=BF,
∵△EBF∽△CBD,
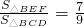
,
∴
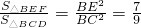
,
∴
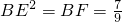
,
∴
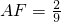
,
∴

,
解得
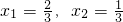
,
∴当

或

时,
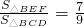
.
解法二:∵△ABC与△BDE都是等边三角形,
∴∠E=∠C=60°,∠EBD=∠CBA=60°,
∴∠EBF=∠CBD,
∴△EBF∽△CBD,
∵
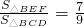
,
∴
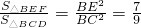
,
∵BC=1,BE=BD,
∴
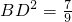
.
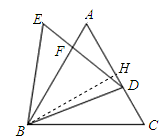
过点B作BH⊥AC于点H,
∵∠C=60°,
∴
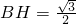
,
∴
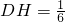
,

,
当点D在线段CH上时,
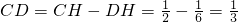
;
当点D在线段CH的延长线上时,
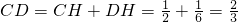
,
综上所述,当

或

时,
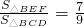
.
分析:(1)由△ABC与△BDE都是等边三角形,可得∠A=∠C=∠BDE=60°,即可得∠ADF=∠DBC,根据有两个角对应相等的三角形相似,可得△BCD∽△DAF;
(2)①根据相似三角形的对应边成比例,可得
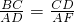
,代入数值,化简即可得y=x-x
2(0<x<1);
②由有两个角对应相等的三角形相似,可得△EBF∽△CBD,由相似三角形的对应边成比例与相似三角形的面积比等于相似比的平方,可得比例式,列方程即可求得.
点评:本题考查了相似三角形的性质与判定.解题时要注意相似三角形的对应边成比例,相似三角形的面积比等于相似比的平方,以及有两个角对应相等的三角形相似.

 如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与A、C重合),DE与AB相交于点F.
如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与A、C重合),DE与AB相交于点F.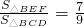 ?
?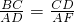 ,
,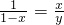 ,
, ,
,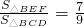 ,
,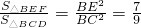 ,
,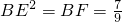 ,
,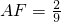 ,
, ,
,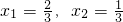 ,
, 或
或 时,
时,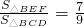 .
.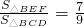 ,
,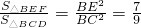 ,
,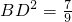 .
.
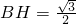 ,
,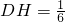 ,
, ,
,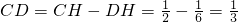 ;
;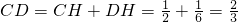 ,
, 或
或 时,
时,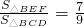 .
.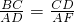 ,代入数值,化简即可得y=x-x2(0<x<1);
,代入数值,化简即可得y=x-x2(0<x<1);

 阅读快车系列答案
阅读快车系列答案