
 小明的爸爸和小明旱晨同时从家出发,以各自的速度匀速步行上班和上学,爸爸前往位于家正东方的公司,小明前往位于家正西方的学校,爸爸到达公司后发现小明的数学作业在自己的公文包里,于是立即跑步去小明,终于在途中追上了小明把作业给了他,然后再以先前的速度步行再回公司(途中给作业的时间忽略不计).结果爸爸回到公司的时间比小明到达学校的时间多用了8分钟.如图是两人之间的距离y(米)与他们从家出发的时间x(分钟)的函数关系图,则小明家与学校相距1800米.
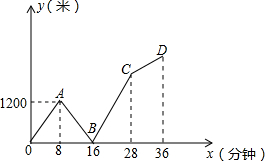
小明的爸爸和小明旱晨同时从家出发,以各自的速度匀速步行上班和上学,爸爸前往位于家正东方的公司,小明前往位于家正西方的学校,爸爸到达公司后发现小明的数学作业在自己的公文包里,于是立即跑步去小明,终于在途中追上了小明把作业给了他,然后再以先前的速度步行再回公司(途中给作业的时间忽略不计).结果爸爸回到公司的时间比小明到达学校的时间多用了8分钟.如图是两人之间的距离y(米)与他们从家出发的时间x(分钟)的函数关系图,则小明家与学校相距1800米. 分析 小明的爸爸回到公司的时间比小明到达学校的时间多用了8分钟,由OA段可知8分钟小明的爸爸正好从家步行到公司,可以推出BC段两人之间的距离正好是家到学校的距离,求出设BC段两人之间的距离即可解决问题.
解答 解:由图象可知,设BC段两人之间的距离为x米,则有$\frac{1200}{8}$=$\frac{x}{12}$,
解得x=1800米,
∵爸爸回到公司的时间比小明到达学校的时间多用了8分钟,由OA段可知8分钟小明的爸爸正好从家步行到公司,
∴BC段两人之间的距离正好是家到学校的距离,
∴小明家与学校相距1800米,
故答案为1800.
点评 本题考查一次函数的应用,一元一次方程的应用等知识,解题的关键是读懂图象信息,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
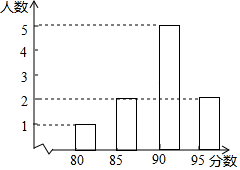 如图,对参加数学竞赛的10名学生的测试成绩进行了统计,对于这10名学生的测试成绩,下列说法错误的是( )
如图,对参加数学竞赛的10名学生的测试成绩进行了统计,对于这10名学生的测试成绩,下列说法错误的是( )| A. | 众数是90 | B. | 中位数是90 | C. | 平均数是90 | D. | 极差是15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
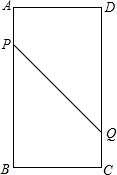 如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2cm/s的速度向点D移动.设运动的时间为t.
如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2cm/s的速度向点D移动.设运动的时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $2<\sqrt{5}<\root{3}{7}$ | B. | $2<\root{3}{7}<\sqrt{5}$ | C. | $\root{3}{7}<2<\sqrt{5}$ | D. | $\sqrt{5}<\root{3}{7}<2$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com