
【题目】解下列方程
(1)![]()
(2)![]()
.
【答案】
(1)
解:去分母得:(x﹣2)2﹣12=x2﹣4,
整理得:x2﹣4x+4﹣12=x2﹣4,
解得:x=﹣1,
经检验x=﹣1是分式方程的解;
(2)
解:去分母得:y﹣2=2y﹣6+1,
解得:y=3,
经检验y=3是增根,分式方程无解.
【解析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;(2)分式方程去分母转化为整式方程,求出整式方程的解得到y的值,经检验即可得到分式方程的解.
【考点精析】解答此题的关键在于理解分式方程的解的相关知识,掌握分式方程无解(转化成整式方程来解,产生了增根;转化的整式方程无解);解的正负情况:先化为整式方程,求整式方程的解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=3,BC=5,点E、F是BC、CD边上的动点(包括端点处),若将纸片沿EF折叠,使得点C恰好落在AD边上点P处.设CF=x,则x的取值范围为 . 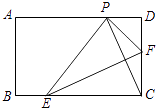
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个如图所示的长方体的透明鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm.一小虫想从鱼缸外的点A处沿缸壁爬到鱼缸内G处吃鱼饵.
(1)小虫应该走怎样的路线才可使爬行的路程最短?请画出它的爬行路线,并用箭头标注;
(2)试求小虫爬行的最短路程.
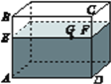
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上. 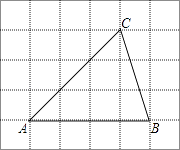
(1)△ABC的面积等于;
(2)若四边形DEFG是△ABC中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.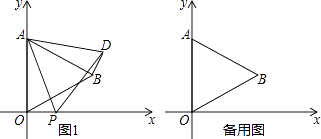
(1)求B的坐标;
(2)当点P运动到点(t,0)时,试用含t的式子表示点D的坐标;
(3)是否存在点P,使△OPD的面积等于 ![]() ,若存在,请求出符合条件的点P的坐标(直接写出结果即可)
,若存在,请求出符合条件的点P的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人从A城出发,前往距离A城30千米的B城.现在有三种方案供他选择:
①骑自行车,其速度为15千米/时;
②蹬三轮车,其速度为10千米/时;
③骑摩托车,其速度为40千米/时.
(1)选择哪种方式能使他从A城到达B城的时间不超过2小时?请说明理由;
(2)设此人在行进途中离B城的距离为s(千米),行进时间为t(时),就(1)所选定的方案,试写出s与t之间的函数关系式(注明自变量t的取值范围),并在如图所示的平面直角坐标系中画出函数的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
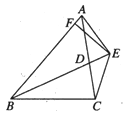
【题目】如图BD为△ABC的角平分线,且BD=BC, E为BD延长线上一点,BE=BA,
过E作EF⊥AB于F,下列结论:
①△ABD≌△EBC ;②∠BCE+∠BDC=180°;
③AD=AE=EC;④AB//CE ;
⑤BA+BC=2BF.其中正确的是________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com