
【题目】除夕夜中央电视台举办的“2016年春节联欢晚会”受到广泛的关注.某组织就“2016年春节联欢晚会”节目的喜爱程度,在三峡广场进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D;根据调查结果绘制出如图所示的扇形统计图(未完成)和条形统计图(未完成),请结合图中所给信息解答下列问题
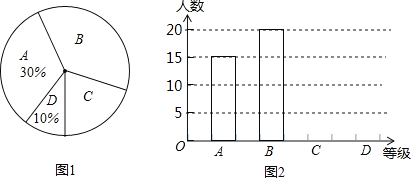
(1)本次被调查对象共有 人;被调查者“不太喜欢”有 人。
(2)将扇形统计图和条形统计图补充完整;
(3)在“非常喜欢”调查结果里有人为80后,其中3男2女,在这5人中,该组织打算随机选2位进行采访,请你用列表法或树状图法求出所选2位恰好都为男性的概率.
【答案】(1)50,5;(2)补图见解析;(3)![]() .
.
【解析】试题分析:(1)根据等级A的人数除以占的百分比求出调查的学生数,进而确定出等级D的人数即可;
(2)求出等级B与C占的百分比,以及等级C与D的人数,补全统计图即可;
(3)列表得出所有等可能的情况数,找出所选两位同学恰好都是男同学的情况数,即可求出所求的概率.
试题解析:(1)本次被调查对象共有:15÷30%=50(人),被调查者“不太喜欢”有:50×10%=5(人);
(2)“感觉一般”的人数为:50-15-20-5=10(人),
C类占:![]() ×100%=20%,B类占:1-30%-20%-10%=40%;
×100%=20%,B类占:1-30%-20%-10%=40%;
如图:
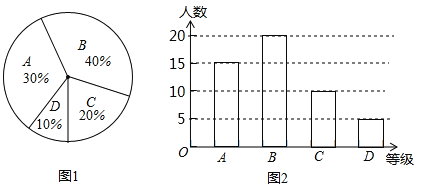
(3)列表如下:
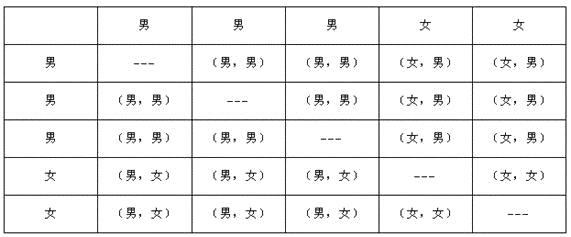
∵所有等可能的情况有20种,其中所选2位同学恰好都是男同学的情况有6种,
∴所选2位恰好都为男性的概率为:![]()


科目:初中数学 来源: 题型:
【题目】已知关于x的方程 x2﹣2x+k=0.
(1)若原方程有实数根,求k的取值范围?
(2)选取一个你喜欢的非零整数值作为k的值,使原方程有实数根,并解方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
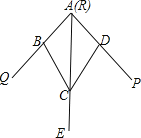
A.SAS
B.ASA
C.AAS
D.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE 沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.
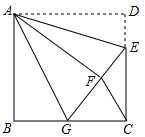
求证:(1)△ABG≌△AFG;
(2)求△FGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的长AB为5,宽BC为4,E是BC边上的一个动点,AE⊥EF,EF交CD于点F.设BE=x,FC=y,则点E从点B运动到点C时,能表示y关于x的函数关系的大致图象是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次献爱心的捐赠活动中,某班45名同学捐款金额统计如下:
金额(元) | 20 | 30 | 35 | 50 | 100 |
学生数(人) | 5 | 10 | 5 | 15 | 10 |
在这次活动中,该班同学捐款金额的众数和中位数分别是( )
A.30,35
B.50,35
C.50,50
D.15,50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com