（6分）如图所示，在△ABC中，AE、BF是角平分线，它们相交于点O，AD是高，∠BAC=50°，∠C=70°，求∠DAC、∠BOA的度数．
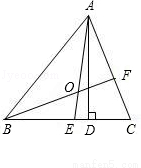
∠DAC=20° ∠BOA=125°.
【解析】
试题分析：根据AD⊥BC，则∠ADC=90°，根据△ADC的内角和可以求出∠DAC的度数，根据△ABC的内角和求出∠ABC的度数，然后根据角平分线的性质求出∠ABO+∠BAO的度数，最后根据△ABO的内角和求出∠BOA的度数.
试题解析：∵AD是高 ∴∠ADC=90° ∵∠C=70°∴∠DAC=180°﹣90°﹣70°=20°
∵∠BAC=50°，∠C=70°，AE是角平分线 ∴∠BAO=25°，∠ABC=60°
∵BF是∠ABC的角平分线 ∴∠ABO=30° ∴∠BOA=180°﹣∠BAO﹣∠ABO=125°
考点：角平分线的性质、角度的计算.
灵星计算小达人系列答案科目：初中数学 来源：2014-2015学年湖南省长沙麓山国际等四校九年级上学期第三次训练数学试卷（解析版） 题型：解答题
在梯形ABCD中，AD∥BC，BA⊥AC，∠ABC = 450，AD = 2，BC = 6，以BC所在直线为x轴，建立如图所示的平面直角坐标系，点A在y轴上.
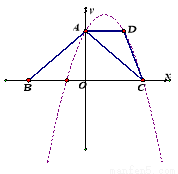
（1）求过A、D、C三点的抛物线的解析式；
（2）求△ADC的外接圆的圆心M的坐标，并求⊙M的半径；
（3）E为抛物线对称轴上一点，F为y轴上一点，求当ED＋EC＋FD＋FC最小时，EF的长；
（4）设Q为射线CB上任意一点，点P为对称轴左侧抛物线上任意一点，问是否存在这样的点P、Q，使得以P、Q、C为顶点的三角形与△ADC相似？若存在，直接写出点P、Q的坐标，若不存在，则说明理由.
查看答案和解析>>
科目：初中数学 来源：2014-2015学年湖南省长沙麓山国际等四校九年级上学期第三次训练数学试卷（解析版） 题型：选择题
将抛物线y=x2﹣6x+5向上平移2个单位长度，再向右平移1个单位长度后，得到的抛物线解析式是（ ）
A．y=（x﹣4）2﹣6 B．y=（x﹣4）2﹣2
C．y=（x﹣2）2﹣2 D．y=（x﹣1）2﹣3
查看答案和解析>>
科目：初中数学 来源：2014-2015学年湖南省长沙麓山国际等四校九年级上学期第三次训练数学试卷（解析版） 题型：选择题
若x：y=1：3，2y=3z，则
的值是（ ）
A．﹣5 B．﹣
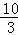C．D．5
查看答案和解析>>
科目：初中数学 来源：2014-2015学年新疆巴州蒙古族中学八年级上学期期末考试数学试卷（解析版） 题型：选择题
如图点A、D、C、E在同一条直线上，AB∥EF，AB=EF，∠B=∠F，AE=10，AC=7，则CD的长为（ ）。
A．5.5 B．4 C．4.5 D．3
查看答案和解析>>
科目：初中数学 来源：2014-2015学年陕西省西安市七年级上学期期末考试数学试卷（解析版） 题型：填空题
已知有理数a, b， c在数轴上的位置如图所示，则化简代数式∣b-c∣-∣c-a∣+∣b-a∣= 。
查看答案和解析>>
科目：初中数学 来源：2014-2015学年辽宁省大石桥市七年级上学期期末考试数学试卷（解析版） 题型：解答题
如图：点A、B、C是数轴上三点，其中点C是线段AB的中点，点O表示的是数轴的原点，线段AC比线段OA长1个单位，点B表示的有理数是17，求点C表示的有理数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
= 。