
在梯形ABCD中,AD∥BC,BA⊥AC,∠ABC = 450,AD = 2,BC = 6,以BC所在直线为x轴,建立如图所示的平面直角坐标系,点A在y轴上.
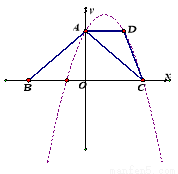
(1)求过A、D、C三点的抛物线的解析式;
(2)求△ADC的外接圆的圆心M的坐标,并求⊙M的半径;
(3)E为抛物线对称轴上一点,F为y轴上一点,求当ED+EC+FD+FC最小时,EF的长;
(4)设Q为射线CB上任意一点,点P为对称轴左侧抛物线上任意一点,问是否存在这样的点P、Q,使得以P、Q、C为顶点的三角形与△ADC相似?若存在,直接写出点P、Q的坐标,若不存在,则说明理由.
(1)由题意知C(3,0)、A(0,3).
如图1,过D作x轴垂线,由矩形性质得D(2,3).
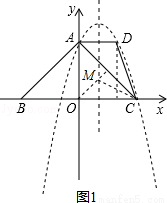
由抛物线的对称性可知抛物线与x轴另一交点为(﹣1,0).
设抛物线的解析式为y=a(x+1)(x﹣3).
将(0,3)代入得a=﹣1,所以 .
.
(2)由外接圆知识知M为对称轴与AC中垂线的交点.
由等腰直角三角形性质得OM平分∠AOC,即yOM=x,
∴M(1,1).
连MC得MC=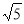 ,即半径为
,即半径为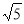 .
.
(3)如图2,
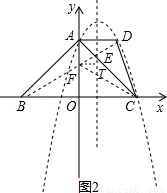
由对称性可知:当ED+EC+FD+FC最小时,E为对称轴与AC交点,F为BD与y轴交点,
∵∠B=45°,∠AOB=90°,
∴AO=BO=3,故B点坐标为:(﹣3,0),
再利用D(2,3),代入y=ax+b,得:
 ,
,
解得: ,
,
故BD直线解析式为: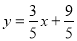 ,
,
当x=0,y= ,根据对称轴为直线x=1,则y=2,
,根据对称轴为直线x=1,则y=2,
故F(0,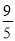 )、E(1,2),
)、E(1,2),
EF=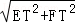 =
=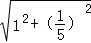 =
= .
.
(4)可得△ADC中,AD=2,AC= ,DC=
,DC=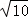 .
.
假设存在,显然∠QCP<90°,则∠QCP=45°或∠QCP=∠CAD.
如图3,
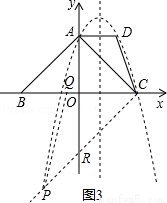
当∠QCP=45°时,OR=OC=3,
则R点坐标为(0,﹣3),将C,R代入y=ax+b得出:
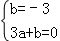 ,
,
解得: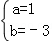 ,
,
这时直线CP的解析式为y=x﹣3,同理可得另一解析式为:y=﹣x+3.
当直线CP的解析式为y=x﹣3时,
则 ,
,
解得: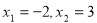 ,
,
可求得P(﹣2,﹣5),
故PC=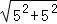 =
=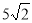 .
.
设CQ=x,则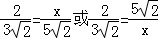 ,
,
解得:x=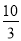 或x=15.
或x=15.
∴Q ( ,0)或(﹣12,0).
,0)或(﹣12,0).
当y=﹣x+3即P与A重合时,CQ=y,则 =
=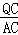 ,
,
即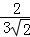 =
= ,或
,或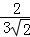 =
=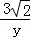 ,
,
解得CQ=2或9,
故Q (1,0)或(﹣6,0).
如图4,
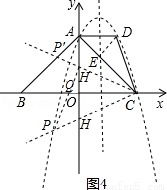
当∠QCP=∠ACD时,设CP交y轴于H,连接ED,则ED⊥AC,
∴DE= ,EC=
,EC=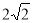 ,
,
易证:△CDE∽△CHQ,
所以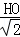 =
= ,
,
∴HO=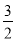 .
.
可求HC的解析式为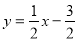 .
.
联解 ,
,
得P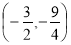 ,PC=
,PC=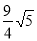 .
.
设CQ=x,知 ,
,
∴x=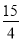 或x=
或x= ,
,
∴Q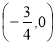 或
或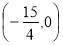 .
.
同理当H在y轴正半轴上时,HC的解析式为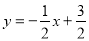 .
.
∴P’ 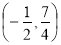 ,
,
∴PC=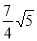
∴ ,
,
∴CQ=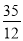 或
或 ,所以Q
,所以Q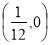 或
或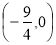 .
.
综上所述,P1(﹣2,﹣5)、Q1( ,0)或(﹣12,0);P2(0,3)、Q2(1,0)或(﹣6,0);P3
,0)或(﹣12,0);P2(0,3)、Q2(1,0)或(﹣6,0);P3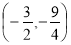 、Q3
、Q3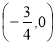 或
或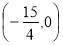 ;P4
;P4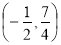 、Q4
、Q4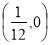 或
或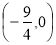 .
.
【解析】
试题分析:(1)过D作x轴垂线,由抛物线的对称性可知抛物线与x轴另一交点为(﹣1,0).再根据交点式即可求出过A、D、C三点的抛物线的解析式;
(2)由外接圆知识知M为对称轴与AC中垂线的交点.由等腰直角三角形性质可得M点的坐标,连MC得MC=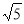 ,即为半径;
,即为半径;
(3)由对称性可知:当ED+EC+FD+FC最小时,E为对称轴与AC交点,F为BD与y轴交点,再根据待定系数法求出BD直线解析式,从而得到E,F的坐标,再根据两点坐标公式即可求得EF的长;
(4)先求出直线CP的解析式为y=x﹣3或y=﹣x+3,再分情况讨论求得以P、Q、C为顶点的三角形与△ADC相似时点P、Q的坐标
考点:二次函数综合题


科目:初中数学 来源:2014-2015学年浙江省温州市九年级上学期期中测试数学试卷(解析版) 题型:解答题
在△ABC中,边BC的长与BC边上的高线长之和为20.
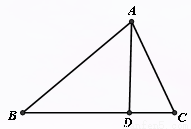
(1)写出△ABC的面积y与BC的长x之间的函数关系式。并写出自变量X的取值范围。
(2)当BC的长为多少时,△ABC的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安市岳池县白庙责任区九年级12月联考数学试卷(解析版) 题型:填空题
如果关于x的二次函数y=x2-2x+k与x轴只有1个交点,则k=_________。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安市岳池县白庙责任区九年级12月联考数学试卷(解析版) 题型:选择题
若n(n≠0)是关于x的方程x2+mx+3n=0的一个根,则m+n的值是( )
A.-3 B.-1 C.1 D.3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省长沙麓山国际等四校九年级上学期第三次训练数学试卷(解析版) 题型:解答题
如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.

(1)求证:△BEF∽△CDF;
(2)求CF的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省长沙麓山国际等四校九年级上学期第三次训练数学试卷(解析版) 题型:填空题
近期随着国家抑制房价新政策的出台,某楼盘房价连续两次下跌,由原来的每平方米10000元降至每平方米8100元,设每次降价的百分率相同,则降价百分率为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年新疆巴州蒙古族中学八年级上学期期末考试数学试卷(解析版) 题型:解答题
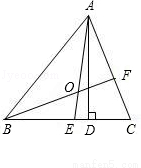
(6分)如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=50°,∠C=70°,求∠DAC、∠BOA的度数.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市七年级上学期期末考试数学试卷(解析版) 题型:选择题
把351000用科学记数法表示,正确的是( )。
(A)0.351×106 (B)3.51×105 (C)3.51×106 (D)35.1×104
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com