
【题目】如图,一次函数![]() 的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°;
的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°;

(1)如果点P(m,![]() )在第二象限内,试用含m的代数式表示四边形AOPB的面积,并求当△APB与△ABC面积相等时m的值;
)在第二象限内,试用含m的代数式表示四边形AOPB的面积,并求当△APB与△ABC面积相等时m的值;
(2)如果△QAB是等腰三角形并且点Q在坐标轴上,请求出点Q所有可能的坐标;
(3)是否存在实数a,b使一次函数![]() 和y=ax+b的图象关于直线y=x对称?若存在,求出
和y=ax+b的图象关于直线y=x对称?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)m=﹣![]() ;(2)Q的坐标为(3,0)或(﹣1,0)或(0,﹣
;(2)Q的坐标为(3,0)或(﹣1,0)或(0,﹣![]() )或(0,
)或(0,![]() +2)或(0,
+2)或(0,![]() ﹣2)或(0,
﹣2)或(0,![]() );(3)见解析
);(3)见解析
【解析】
试题分析:(1)过点P作PD⊥x轴于D,根据一次函数解析式求出点A、B的坐标,从而求出OA、OB,利用勾股定理列式求出AB,然后求出∠ABO=30°,再根据S四边形AOPB=S梯形PDOB+S△AOB﹣S△PDO列式整理即可得解;根据S△APB=S四边形AOPB﹣S△AOP表示出△APB的面积,再解直角三角形求出AC,然后求出△ABC的面积,列出方程求解即可;
(2)分①点A是顶角顶点,AB是腰时,求出OQ的长度,②点B是顶角顶点,AB是腰时,求出OQ的长度,然后写出点Q的坐标,③AB是底边时,分点Q在y轴上和点Q在x轴上两种情况,利用等边三角形的性质求解;
(3)求出A、B两点关于直线y=x的对称点的坐标,再利用待定系数法求一次函数解析式求出a、b,然后代入代数式进行计算即可得解.
解:(1)如图,过点P作PD⊥x轴于D,
∵点P(m,![]() )在第二象限内,
)在第二象限内,
∴PD=![]() ,OD=﹣m,
,OD=﹣m,
令y=0,则﹣![]() x+
x+![]() =0,
=0,
解得x=1,
令x=0,则y=![]() ,
,
∴点A(1,0),B(0,![]() ),
),
∴OA=1,OB=![]() ,
,
由勾股定理得,AB=![]() =
=![]() =2,
=2,
∴∠ABO=30°,
S四边形AOPB=S梯形PDOB+S△AOB﹣S△PDO,
=![]() ×(
×(![]() +
+![]() )(﹣m)+
)(﹣m)+![]() ×1×
×1×![]() ﹣
﹣![]() ×(﹣m)×
×(﹣m)×![]() ,
,
=﹣![]() m+
m+![]() ,
,
∴四边形AOPB的面积=﹣![]() m+
m+![]() ;
;
S△APB=S四边形AOPB﹣S△AOP,
=﹣![]() m+
m+![]() ﹣
﹣![]() ×1×
×1×![]() ,
,
=﹣![]() m+
m+![]() ,
,
∵∠ABC=30°,
∴AC=ABtan30°=2×![]() =
=![]() ,
,
∴S△ABC=![]() ×2×
×2×![]() =
=![]() ,
,
∵△APB与△ABC面积相等,
∴﹣![]() m+
m+![]() =
=![]() ,
,
解得m=﹣![]() ,
,
故,当△APB与△ABC面积相等时,m=﹣![]() ;
;
(2)①点A是顶角顶点,AB是腰时,AQ=AB=2,
若点Q在x正半轴,则OQ=AO+AQ=1+2=3,
若点Q在x轴负半轴,则OQ=AQ﹣AO=2﹣1=1,
若点Q在y轴负半轴,则OQ=BO=![]() ,
,
∴点Q的坐标为(3,0)或(﹣1,0)或(0,﹣![]() ),
),
②点B是顶角顶点,AB是腰时,BQ=AB=2,
若点Q在y轴正半轴,则OQ=BO+BQ=![]() +2,
+2,
若点Q在y轴负半轴,则OQ=BQ﹣BO=2﹣![]() ,
,
若点Q在x轴负半轴,则OQ=AO=1,
∴点Q的坐标为(0,![]() +2)或(0,
+2)或(0,![]() ﹣2)或(﹣1,0);
﹣2)或(﹣1,0);
③AB是底边时,若点Q在y轴上,则OQ=OAtan30°=1×![]() =
=![]() ,
,
若点Q在x轴上,则OQ=AO=1,
∴点Q的坐标为(0,![]() )或(﹣1,0),
)或(﹣1,0),
综上所述,△QAB是等腰三角形时,坐标轴上点Q的坐标为(3,0)或(﹣1,0)或(0,﹣![]() )或(0,
)或(0,![]() +2)或(0,
+2)或(0,![]() ﹣2)或(0,
﹣2)或(0,![]() );
);
(3)∵A(1,0)关于y=x的对称点为(0,1),
B(0,![]() )关于y=x的对称点为(
)关于y=x的对称点为(![]() ,0),
,0),
∴![]() ,
,
解得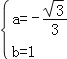 ,
,
∴![]() =
= =
=![]() ,
,
=![]() ,
,
=![]() ,
,
=﹣![]() .
.



科目:初中数学 来源: 题型:
【题目】小明设计了一个魔术盒,当任意实数对(a,b)进入其中,会得到一个新的实数a2-2b+3,若将实数对(x,-2x)放入其中,得到一个新数为8,则x=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“Welcome to Senior High School.”(欢迎进入高中),在这段句子的所有英文字母中,字母o出现的频率是( )
A. 0.2 B. 0.4 C. 0.6 D. 0.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知, ![]() ∥
∥![]() ,
, ![]() ,试解答下列问题:
,试解答下列问题:
(1)如图①,则![]() __________,则OB与AC的位置关系为__________
__________,则OB与AC的位置关系为__________

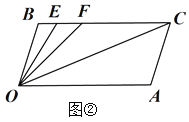
(2)如图②,若点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,并且
,并且![]() 平分
平分![]() .则
.则![]() 的度数等于_____________;
的度数等于_____________;
(3)在第(2)题的条件下,若平行移动![]() 到如图③所示位置.
到如图③所示位置.
①在AC移动的过程中, ![]() 与
与![]() 的比值是否发生改变,若不改变求出其比值,若要改变说明理由;
的比值是否发生改变,若不改变求出其比值,若要改变说明理由;
②当∠OEB=∠OCA时,求∠OCA

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180,∠A=∠C,DA平分∠BDF。
(1)求证:AE∥FC.
(2)AD与BC的位置关系如何,为什么?
(3)证明:BC平分∠DBE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com