
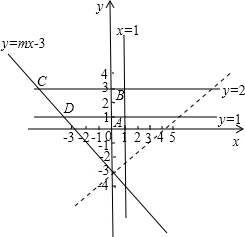
 解:如图,
解:如图, ,3),D(
,3),D( ,1),AB=2,四边形ABCD为直角梯形,
,1),AB=2,四边形ABCD为直角梯形, ,AD=1-
,AD=1- ,
, ×AB×(BC+AD)=12,
×AB×(BC+AD)=12, •2•(1-
•2•(1- +1-
+1- )=12,
)=12, =-1,解得m=-1,经检验是原方程的解.
=-1,解得m=-1,经检验是原方程的解. -1,AD=
-1,AD= -1,
-1, •2•(
•2•( -1+
-1+ -1)=12,
-1)=12, =7,解得m=
=7,解得m= ,经检验是原方程的解.
,经检验是原方程的解. .
. .
. ,1),C(
,1),C( ,3);然后讨论m>0,或m<0,分别表示出AD和BC的长,用直角梯形的面积建立方程,解方程可得到m的值.
,3);然后讨论m>0,或m<0,分别表示出AD和BC的长,用直角梯形的面积建立方程,解方程可得到m的值.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 (2013•黄陂区模拟)已知:抛物线y=x2+mx+n的顶点D(1,-4)抛物线与坐标轴的交点为A,B,C,
(2013•黄陂区模拟)已知:抛物线y=x2+mx+n的顶点D(1,-4)抛物线与坐标轴的交点为A,B,C,| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:抛物线y=x2+mx+n的顶点D(1,-4)抛物线与坐标轴的交点为A,B,C,
已知:抛物线y=x2+mx+n的顶点D(1,-4)抛物线与坐标轴的交点为A,B,C, ,MN是直线y=-x上的一条动线段,当四边形AMNC的周长最小时,求N的坐标.
,MN是直线y=-x上的一条动线段,当四边形AMNC的周长最小时,求N的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com