练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．若|1-x|=1+|x|，则$\sqrt{（x-1）^{2}}$=1-x．

    分析 根据绝对值的性质求出x的范围，根据二次根式的性质化简即可．

    解答 解：∵|1-x|=1+|x|，
    ∴x≤0，
    ∴$\sqrt{（x-1）^{2}}$=1-x，
    故答案为：1-x．

    点评 本题考查的是二次根式的化简，掌握二次根式的性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．某物流公司现有31吨货物运往某地，计划同时租用A型车a辆，B型车b辆，使每辆车都装满货物恰好一次运完．
    已知每种型号车的载重量和租金如表：
    车型AB
    载重量（吨/辆）34
    租金（元/辆）10001200
    （1）请你帮该物流公司设计租车方案；
    （2）请选出最省钱的租车方案，并求出最少租车费．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

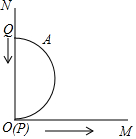    15．如图，己知射线OM与射线ON互相垂直，A是直径PQ为2cm的半圆铁片上一点，且弧AQ的度数为60°，（即弧AQ所对的圆心角为60°）动点P从点O沿射线OM开始滑动，同时动点Q在ON上滑动，当点Q滑至点O停止时，点A所经过的路程是（　　）
    A．3B．3-$\sqrt{3}$C．3+$\sqrt{3}$D．6-2$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算：（-$\frac{3}{2}$）2÷（-$\frac{1}{2}$）2×（1$\frac{1}{3}$）2-（-4）2-42．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．如图1，在边长为4的正△ABC中，点P以每秒1cm的速度从点A出发，沿折线AB-BC运动，到点C停止．过点P作PD⊥AC，垂足为D，PD的长度y（cm）与点P的运动时间x（秒）的函数图象如图2所示．当点P运动5.5秒时，PD的长是（　　）
    A．$\frac{5\sqrt{3}}{4}$cmB．$\frac{5\sqrt{3}}{2}$cmC．2$\sqrt{3}$cmD．3$\sqrt{3}$cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，有一块四边形形状的铁皮ABCD，BC=CD=6，AB=2AD，∠ABC=∠ADB=90°，以C为圆心，CB为半径作弧BD得一扇形CBD，剪下扇形并用它围成一圆锥的侧面．
    求：（1）∠BCD的度数；
    （2）该圆锥的底面半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

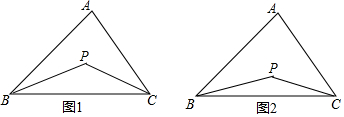    16．【提出问题】已知如图1，P是∠ABC、∠ACB的角平分线的交点，你能找到∠P、∠A的关系吗？
    【分析问题】在解决这个问题时，某小组同学是这样做的：
    先赋予∠A几个特殊值：
    当∠A=80°时，计算出∠P=130°；
    当∠A=40°时，计算出∠P=110°；
    当∠A=100°时，计算出∠P=140°；
    …由以上特例猜想∠P与∠A的关系为：∠P=90°+$\frac{1}{2}$∠A．再证明这一结论：
    证明：∵点P是∠ABC、∠ACB的角平分线的交点．
    ∴∠PBC=$\frac{1}{2}$∠ABC；∠PCB=$\frac{1}{2}$∠ACB
    ∴∠PBC+∠PCB=$\frac{1}{2}$（∠ABC+∠ACB）
    又∵∠A+（∠ABC+∠ACB）=180°
    ∴∠ABC+∠ACB=180°-∠A
    ∴∠PBC+∠PCB=$\frac{1}{2}$（∠ABC+∠ACB）
    =$\frac{1}{2}$（180°-∠A）
    ∴∠P=180°-（∠PBC+∠PCB）
    =180°-$\frac{1}{2}$（180°-∠A）
    =90°+$\frac{1}{2}$∠A
    【解决问题】请运用以上解决问题的“思想方法”解决下面的几个问题：
    （1）如图2，若点P时∠ABC、∠ACB的三等分线的交点，即∠PBC=$\frac{1}{3}$∠ABC，∠PCB=$\frac{1}{3}$∠ACB，猜测∠P与∠A的关系为∠P=$\frac{1}{3}$∠A+$\frac{2}{3}$×180°，证明你的结论．
    （2）若点P时∠ABC、∠ACB的四等分线的交点，即∠PBC=$\frac{1}{4}$∠ABC，∠PCB=$\frac{1}{4}$∠ACB，则∠P与∠A的关系为∠P=$\frac{1}{4}$∠A+$\frac{3}{4}$×180°．（直接写出答案，不需要证明）
    （3）若点P时∠ABC、∠ACB的n等分线的交点，即∠PBC=$\frac{1}{n}$∠ABC，∠PCB=$\frac{1}{n}$∠ACB，则∠P与∠A的关系为$\frac{n-1}{n}$•180°+$\frac{1}{n}$∠A．（直接写出答案，不需要证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图所示，直线AD和BC被直线AB所截，∠1和∠2是同位角；∠4、∠FAC与∠2也是同位角．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．画出函数y=2x+1的图象，利用图象求：
    （1）求方程2x+1=0的解；
    （2）求出不等式2x+1≥0的解集；
    （3）当-3≤y≤3时，求x的取值范围；
    （4）求图象与坐标轴围成的三角形面积．

    查看答案和解析>>

    同步练习册答案