
 顺时针连续翻转3n次,点A经过的路径长为________;顺时针连续翻转3n+1次,点A经过的路径长为________.
顺时针连续翻转3n次,点A经过的路径长为________;顺时针连续翻转3n+1次,点A经过的路径长为________.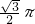 cm
cm 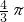 cm
cm 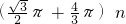 cm
cm 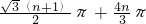 cm
cm cm,
cm,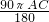 =
=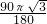 =
=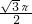 cm;
cm; =
= cm;
cm;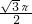 +
+ ,旋转的过程中每3次循环一次,
,旋转的过程中每3次循环一次,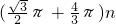 cm.
cm.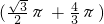 n+
n+ π=
π=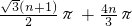 cm.
cm.

科目:初中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
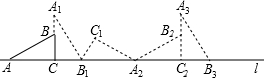 顺时针连续翻转3n次,点A经过的路径长为
顺时针连续翻转3n次,点A经过的路径长为
| ||
| 2 |
| 4 |
| 3 |
| ||
| 2 |
| 4 |
| 3 |
| ||
| 2 |
| 4n |
| 3 |
| ||
| 2 |
| 4n |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
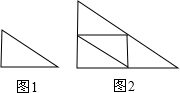 (2013•龙湾区一模)小明拿三角板来玩,他发现用四块(大小一样)含30°角的直角三角板(如图1),可以拼成一个更大的含30°角的直角三角形(如图2).若要在图2的基础上,拼成一个比图2更大的含30°角的直角三角形,则至少还需含30°角的直角三角板(如图1)的个数为( )
(2013•龙湾区一模)小明拿三角板来玩,他发现用四块(大小一样)含30°角的直角三角板(如图1),可以拼成一个更大的含30°角的直角三角形(如图2).若要在图2的基础上,拼成一个比图2更大的含30°角的直角三角形,则至少还需含30°角的直角三角板(如图1)的个数为( )查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC是等腰直角三角形,△DEF是一个含30°角的直角三角形,将D放在BC的中点上,转动△DEF,设DE,DF分别交AC,BA的延长线于E,G,则下列结论:
如图,△ABC是等腰直角三角形,△DEF是一个含30°角的直角三角形,将D放在BC的中点上,转动△DEF,设DE,DF分别交AC,BA的延长线于E,G,则下列结论:| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com