Question

17．请根据所给信息，帮助小樊同学完成他的调查报告

调查目的	了解八年级学生每天干家务活的平均时间
调查内容	秦淮区某中学八年级学生每天干家务活的平均时间
调查方式	抽样调查
调查步骤	1、数据的收集： （1）在秦淮区某中学八年级每班随机调查5名学生； （2）统计这些学生2014年4月每天干家务活的平均时间（单位：min）， 结果如下（其中A表示10min；B表示20min；C表示30min）；   B A A B B B B A C B B A B B C A B A A C A B B C B A B B A C 2、数据的处理： 以频数分布直方图的形式呈现上述统计结果，请补全频数分布直方图   3、数据的分析 列式计算所随机调查学生每天干家务活平均时间的平均数（结果保留整数）
调查结论	秦淮区某中学八年级共有450名学生，其中大约有225名学生每天干家务活的平均时间是20min …

Answer 1

分析 先从图表中得出平均每天干家务活在30min的有5名学生，从而补全统计图，再根据A表示10min，B表示20min，C表示30min和学生数即可求出随机调查的学生每天干家务活的平均时间，最后根据每天干家务活的平均时间是20min所占的百分比乘以450，即可得出大约每天干家务活的平均时间是20min的学生数．

解答 解：从图表中可以看出C的学生数是5人，如图：
 
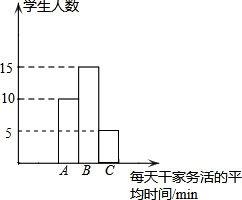
每天干家务活平均时间是：（10×10+15×20+5×30）÷30≈18（min）；  
根据题意得：450×$\frac{15}{30}$=225（人），
秦淮区某中学八年级共有450名学生，其中大约有225名学生每天干家务活的平均时间是20min； 
故答案为：225．

点评 本题考查了频率分布直方图、加权平均数以及用样本估计总体，解题的关键是读懂统计图，从统计图中获取必要的信息，认真观察、分析、研究统计图，才能作出正确的判断和解决问题．