
分析 过C作CD⊥AB于D,由AC:AB=$\sqrt{2}$:3,设AC=$\sqrt{2}$,AB=3,CD=x,根据tanB=1:2,求得BD=2x,根据勾股定理得到AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{2-{x}^{2}}$,根据AD+BD=AB,列方程$\sqrt{2-{x}^{2}}$+2x=3,解得x=1或x=$\frac{7}{5}$,即可得到结果.
解答 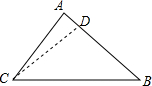 解:如图,过C作CD⊥AB于D,
解:如图,过C作CD⊥AB于D,
∵AC:AB=$\sqrt{2}$:3,
∴设AC=$\sqrt{2}$,AB=3,CD=x,
∵tanB=1:2,
∴BD=2x,
AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{2-{x}^{2}}$,
∴AD+BD=AB,即$\sqrt{2-{x}^{2}}$+2x=3,
解得x=1或x=$\frac{7}{5}$,
∴tanA=$\frac{CD}{AD}$=1或tanA=$\frac{CD}{AD}$=7,
故答案为:1或7.
点评 本题考查了解直角三角形,熟记解直角三角形的定义是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 调查目的 | 了解八年级学生每天干家务活的平均时间 | ||||||||||||||||||||||||||||||
| 调查内容 | 秦淮区某中学八年级学生每天干家务活的平均时间 | ||||||||||||||||||||||||||||||
| 调查方式 | 抽样调查 | ||||||||||||||||||||||||||||||
| 调查步骤 | 1、数据的收集: (1)在秦淮区某中学八年级每班随机调查5名学生; (2)统计这些学生2014年4月每天干家务活的平均时间(单位:min), 结果如下(其中A表示10min;B表示20min;C表示30min);
以频数分布直方图的形式呈现上述统计结果,请补全频数分布直方图  3、数据的分析 列式计算所随机调查学生每天干家务活平均时间的平均数(结果保留整数) | ||||||||||||||||||||||||||||||
| 调查结论 | 秦淮区某中学八年级共有450名学生,其中大约有225名学生每天干家务活的平均时间是20min … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com