
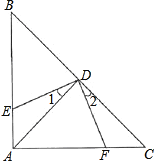
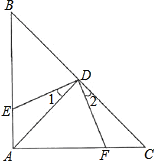
【题目】如图:△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF.
(1)∠1=∠2吗?为什么?
(2)△ADE与△CDF全等吗?为什么?
(3)若AB=8cm,求四边形AEDF的面积.
【答案】(1)相等,理由见解析;(2)全等,理由见解析;(3)16平方厘米.
【解析】试题分析:(1)利用公共角证明∠1=∠2.
(2)利用直角三角形斜边中线是斜边一半得到AD=CD,∠C=∠DAC, ∠1=∠2,利用ASA证明
△ADE与△CDF全等.
(3)利用(2)的结论,割补法,四边形面积恰好是等腰三角形面积一半.
(1)∵AB=AC,D是BC的中点,
∴∠ADC=90 ,
∴∠2+∠ADF=90,
∵DE⊥DF ,
∴∠1+∠ADF=90,
∴∠1=∠2 .
(2) ∵△ABC是等腰直角三角形,
∴∠C=45,
∵AB=AC,D是BC的中点.
∴∠DAC=∠DAE=45°,
∴DA=DC,
在△ADE与△CDF中,
∠EAD=∠C=45 , DA=DC , ∠1=∠2,
∴△ADE≌△CDF.
(3)由(2)△ADE≌△CDF,
∴S△AED=S△CDF,
∵S四边形AEDF=S△ADE+S△ADF,
∴S四边形AEDF=S△CDF+S△ADF =S△ADC,
= ![]() S△ABC,,
S△ABC,,
= ![]() ×8×8=16(㎝2).
×8×8=16(㎝2).


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】已知α、β都是锐角,如果sinα=cosβ,那么α与β之间满足的关系是( )
A.α=β;
B.α+β=90°;
C.α-β=90°;
D.β-α=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是 (只需填序号即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班抽取6名同学参加体能测试,成绩如下:80,90,75,75,80,80.下列表述错误的是( )
A. 众数是80 B. 中位数是75 C. 平均数是80 D. 极差是15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD各个顶点的坐标分别为(﹣2,8),(﹣11,6),(﹣14,0),(0,0).
(1)求这个四边形的面积.
(2)如果把原来的四边形ABCD向下平移3个单位长度,再向左平移2个单位长度后得到新的四边形A1B2C3D4 , 请直接写出平移后的四边形各点的坐标和新四边形的面积.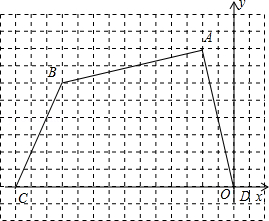
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动手操作,探究:
探究一:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系.
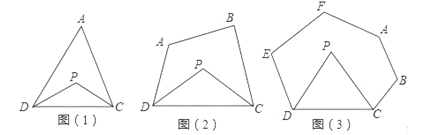
已知:如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.并说明理由.
探究二:若将△ADC改为任意四边形ABCD呢?
已知:如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,请你利用上述结论探究∠P与∠A+∠B的数量关系,并说明理由.
探究三:若将上题中的四边形ABCD改为六边形ABCDEF如图(3)所示,请你直接写出∠P与∠A+∠B+∠E+∠F的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.在同一平面内,过直线外一点,有无数条直线与已知直线垂直
B.由平移得到的两个图形的各组对应点连线互相垂直
C.命题“一个角的余角一定是锐角”是真命题
D.![]() 是无理数
是无理数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com