
����Ŀ�����ֲ�����̽����
̽��һ�������ε�һ���ڽ����������ڽǵ�ƽ�������еĶ۽�֮���к��ֹ�ϵ��
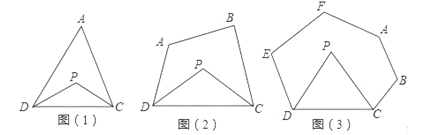
��֪����ͼ��1��������ADC����DP��CP�ֱ�ƽ����ADC����ACD����̽����P����A��������ϵ����˵��������
̽������������ADC��Ϊ�����ı���ABCD�أ�
��֪����ͼ��2�������ı���ABCD����DP��CP�ֱ�ƽ����ADC����BCD������������������̽����P����A+��B��������ϵ����˵��������
̽���������������е��ı���ABCD��Ϊ������ABCDEF��ͼ��3����ʾ������ֱ��д����P����A+��B+��E+��F��������ϵ��
���𰸡�̽��һ�� 90��+![]() ��A��̽������
��A��̽������![]() ����A+��B����̽��������P=
����A+��B����̽��������P=![]() ����A+��B+��E+��F����180�㣮
����A+��B+��E+��F����180�㣮
�����������������
̽��һ�����ݽ�ƽ���ߵĶ���ɵá�PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��ACD��Ȼ������������ڽǺͶ�����ʽ�������ɵý�.
��ACD��Ȼ������������ڽǺͶ�����ʽ�������ɵý�.
̽�����������ı��ε��ڽǺͶ�����ʾ����ADC+��BCD��Ȼ��ͬ��̽��һ���.
̽���������������ε��ڽǺ�ʽ��ʾ����EDC+��BCD��Ȼ��ͬ��̽��һ���.
���������
̽��һ����DP��CP�ֱ�ƽ�֡�ADC�͡�ACD��
���PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��ACD��
��ACD��
���DPC=180��-��PDC-��PCD��
=180��-![]() ��ADC-
��ADC-![]() ��ACD��
��ACD��
= 180��-![]() ����ADC+��ACD����
����ADC+��ACD����
=180��-![]() ��180��-��A����
��180��-��A����
=90��+![]() ��A��
��A��
̽��������DP��CP�ֱ�ƽ�֡�ADC�͡�BCD��
���PDC=![]() ��ADC����PCD=
��ADC����PCD=![]() ��BCD��
��BCD��
���DPC=180��-��PDC-��PCD��
=180��-![]() ��ADC-
��ADC-![]() ��BCD��
��BCD��
=180��-![]() ����ADC+��BCD����
����ADC+��BCD����
=180��-![]() ��360��-��A-��B����
��360��-��A-��B����
=![]() ����A+��B����
����A+��B����
̽������������ABCDEF���ڽǺ�Ϊ����6-2����180��=720�㣬
��DP��CP�ֱ�ƽ�֡�EDC�͡�BCD��
���PDC=![]() ��EDC����PCD=
��EDC����PCD=![]() ��BCD��
��BCD��
���P=180��-��PDC-��PCD��
=180��-![]() ��EDC-
��EDC-![]() ��BCD��
��BCD��
=180��-![]() ����EDC+��BCD����
����EDC+��BCD����
=180��-![]() ��720��-��A-��B-��E-��F����
��720��-��A-��B-��E-��F����
=![]() ����A+��B+��E+��F��-180�㣬
����A+��B+��E+��F��-180�㣬
����P=![]() ����A+��B+��E+��F��-180����
����A+��B+��E+��F��-180����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ӹ������ξֻ�Ϥ��2017�괺���ڼ䣬ȫ�����Ӵ��ο�3.44���˴Σ�ʵ������������423300000000Ԫ����423300000000Ԫ�ÿ�ѧ��������ʾΪ�� ��
A.4.233��103Ԫ
B.0.4233��104Ԫ
C.42.33��1010Ԫ
D.4.233��1011Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
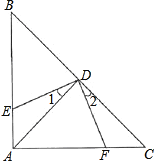
����Ŀ����ͼ����ABC�У���BAC=90�㣬AB=AC����D��б��BC���е㣬DE��DF��
��1����1=��2��Ϊʲô��
��2����ADE����CDFȫ����Ϊʲô��
��3����AB=8cm�����ı���AEDF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������۶Ϣ١�1=��2���ڡ�B=��D���ۡ�A=��C���������ѡ������Ϊ��������һ����Ϊ���۹���һ�����⣬��֤�����������ȷ�ԣ� 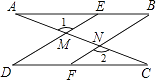
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
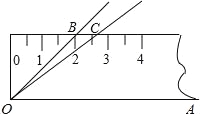
����Ŀ����ͼ����45������AOB������ķ�ʽ������һ�ѿ̶ȳ��ϣ�����O������صĶ˵��غϣ�OA��������غϣ�OB������صĽ���B�ڳ��ϵĶ���ǡΪ2cm��������ͬ�ķ�ʽ��37������AOC�����ڸÿ̶ȳ��ϣ���OC������صĽ���C�ڳ��ϵĶ���ԼΪ cm���������ȷ��0.1cm���ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���¹ڷ������鷢���������ҹ������������ģ���ͬŬ���������飬��ȡ����ʤ������ֹ3��13�գ��ҹ������������ŵ��������Ͷ���Ѿ��ﵽ��1169��Ԫ��1169��Ԫ�ÿ�ѧ��������ʾΪ_____Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A����5��0����B��3��0����
��1����y������һ��C��ʹ֮����S��ABC=16�����C�����꣨Ҫ�б�Ҫ�IJ��裩��
��2����ֱ������ƽ������һ��C��������S��ABC=16��C�ж��ٸ�����Щ����ʲô������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�������ȷ���ǣ� ��
A.3a2+2a2=5a4
B.��2a2��a2=4
C.��2a2��3=2a6
D.a��a��b+1��=a2��ab
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н��ۣ����������������ϵĵ���һһ��Ӧ�ģ����������������ϵĵ���һһ��Ӧ�ģ���ʵ���������ϵĵ���һһ��Ӧ�ģ�����ƽ��ֱ������ϵ�У�ƽ���ϵĵ�������ʵ����֮����һһ��Ӧ�ģ�������ȷ�Ľ��۹��У�������
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com