
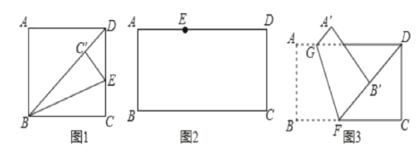
����Ŀ��(1)��ͼ1��������ABCD�۵���ʹBC���ڶԽ���BD�ϣ��ۺ�ΪBE����C���ڵ�C'��������ADB=46�������DBE�Ķ���Ϊ______.
(2)С��������һ�ž���ֽƬABCD��AB=4��AD=9��
����һ����
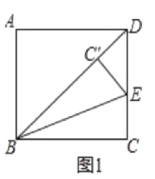
��ͼ2����E�����ž���ֽƬ�ı�AD�ϣ���ֽƬ�۵���ʹAB����CE����ֱ���ϣ��ۺ���ΪMN(��M��N�ֱ��ڱ�AD��BC��)������ֱ�ߺ�Բ�滭���ۺ�MN(��д������������ͼ�ۼ������ú�ɫˮ�ʰ��߶������)��
����һ�㣩
��ͼ3����F�����ž���ֽƬ�ı�BC�ϣ���ֽƬ�۵���ʹFB��������FD�ϣ��ۺ�ΪGF����A��B�ֱ����ڵ�A'��B'������AG=![]() ����B'D�ij���
����B'D�ij���
���𰸡�(1)23(2)����һ������ͼ������;����һ�㡿DB`=3
��������
(1)���ݾ������ʿɵ�AD��BC,�Ӷ��ɵá�ADB=��DBC=46��,�ٸ��ݷ��۵����ʼ�����á�DBE�Ķ�
(2)��һ��:����CE���ӳ���BA���ӳ������G,���ó߹���ͼ������BGC�Ľ�ƽ�����ɵ�ץ��MN,
��һ��:����֪�ɵ�GD=![]() ,���ݾ��ε����ʼ����۵����ʿɵá�DFG=��DGF,�Ӷ��ɵ�DF=DG=
,���ݾ��ε����ʼ����۵����ʿɵá�DFG=��DGF,�Ӷ��ɵ�DF=DG=![]() ,��Rt��CDE��,���ݹ��ɶ��������CF=
,��Rt��CDE��,���ݹ��ɶ��������CF=![]() ,����BF=BC-CF���BF�ij�,�ٸ��ݷ��۵����ʼ̶������DB`�ij�����
,����BF=BC-CF���BF�ij�,�ٸ��ݷ��۵����ʼ̶������DB`�ij�����
(1)��ͼ1�У�
���ı���ABCD�Ǿ��Σ�
��AD//BC��
���ADB=��DBC=46����
�ɷ��۲����Կ�֪����DBE=��EBC=![]() ��DBC=23����
��DBC=23����
�ʴ�Ϊ23��
(2)����һ��������ͼ2�У�

����һ�㡿
��ͼ3�У�
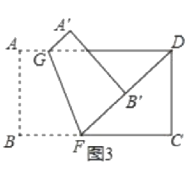
��AG=![]() ��AD=9��
��AD=9��
��GD=9![]() =
=![]() ��
��
���ı���ABCD�Ǿ��Σ�
��AD//BC��
���DGF=��BFG��
�ɷ��۲����Կ�֪����BFG=��DFG��
���DFG=��DGF��
��DF=DG=![]() ��
��
��CD=AB=4����C=90����
����Rt��CDF��CF=![]() ��
��
��BF=BCCF=![]() ��
��
�ɷ��۲����Կ�֪��FB=FB'=![]() ��
��
��DB'=DFFB'=![]()
![]() =3��
=3��


 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д� �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
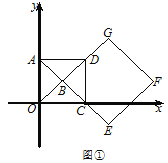
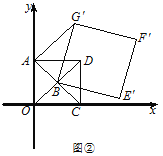
����Ŀ����ƽ��ֱ������ϵ�У�![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() ��0��1������
��0��1������![]() ��1��0����������
��1��0����������![]() �������Խ��ߵĽ���Ϊ
�������Խ��ߵĽ���Ϊ![]() ���ӳ�
���ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() ���ӳ�
���ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() ����
����![]() ��
��![]() Ϊ�ڱ���������
Ϊ�ڱ���������![]() ��
��
������ͼ�٣���![]() �ij���
�ij���![]() ��ֵ��
��ֵ��
������ͼ�ڣ�������![]() �̶�����������
�̶�����������![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת����������
��ʱ����ת����������![]() ������ת��Ϊ
������ת��Ϊ![]() ��0�㣼
��0�㣼![]() ��360�㣩������
��360�㣩������![]() ��
��
����ת�����У���![]() 90��ʱ����
90��ʱ����![]() �Ĵ�С��
�Ĵ�С��
������ת�����У���![]() �ij�ȡ���ֵʱ����
�ij�ȡ���ֵʱ����![]() �����꼰��ʱ
�����꼰��ʱ![]() �Ĵ�С��ֱ��д��������ɣ���
�Ĵ�С��ֱ��д��������ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��y=��![]() x+12��x�ᣬy��ֱ��ཻ�ڵ�A��B����ABO��ƽ������x���ཻ�ڵ�C��
x+12��x�ᣬy��ֱ��ཻ�ڵ�A��B����ABO��ƽ������x���ཻ�ڵ�C��
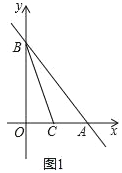
��1����ͼ1�����C�����ꣻ
��2����ͼ2����D��E��F�ֱ����߶�BC��AB��OB�ϣ���D��E��F�������B�غϣ�������DE��DF��EF���ҡ�EDF+��OBC=90������֤����FED=��AED��
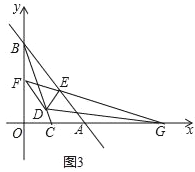
��3����ͼ3���ڣ�2���������£��ӳ��߶�FE��x���ཻ�ڵ�G������DG������CGD=��FGD��BF��BE=5��8����ֱ��DF�Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������̳�������ͬ��ij����Ʒ��ÿ���ۼ۾�Ϊ3000Ԫ�����Ҷ�����һ�����Żݣ����̳����Ż������ǣ���һ����ԭ�ۼ��շѣ�����ÿ���Ż�30%�����̳����Ż������ǣ�ÿ���Ż�25%����������ƷΪx��ʱ�����̳��շ�Ϊy1Ԫ�����̳��շ�Ϊy2Ԫ��
��1���ֱ����y1��y2��x֮��Ĺ�ϵʽ��
��2�����ס��������̳����շ���ͬʱ��������ƷΪ���ټ���
��3����������ƷΪ5��ʱ��Ӧѡ���ĸ��̳����Żݣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���糿��С������ͨ��ѧУΨһ��һ��·��ֱ·����ѧ��;�з����������У�ͣ�����������绰������ӵ��绰����Ϸ������ϸ���ѧУ��ͬʱС�շ��أ�����������С����������ѧУ������ؼң�15���Ӻ����赽�ң��پ���3����С�յ���ѧУ��С��ʼ����100��/�ֵ��ٶȲ��У�С�պ�����ľ���y����λ���ף���С�մ���绰��IJ���ʱ��t����λ���֣�֮��ĺ�����ϵ��ͼ����������˵���д�����ǣ� ��

A. ��绰ʱ��С�պ�����ľ���Ϊ1250��
B. ����绰����23����С�յ���ѧУ
C. С�պ���������������ؼҵ��ٶ�Ϊ150��/��
D. С�ռ���ѧУ�ľ���Ϊ2550��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����װ���ϰ���4500Ԫ����һ��ij��T�������������ܹ˿�ϲ�����ܿ����꣬�ϰ�����4950Ԫ�����ڶ����ÿ�ʽT�����������������һ����ͬ����ÿ�����۱ȵ�һ������9Ԫ��
��1����һ���ÿ�ʽT����ÿ�������Ƕ���Ԫ��
��2���ϰ���ÿ��120Ԫ�ļ۸����۸ÿ�ʽT���������ڶ���T�����۳�![]() ʱ�����������������Ǿ������۴�������Ҫʹ�ڶ���������������650Ԫ��ʣ���T����ÿ���ۼ�����Ҫ����Ԫ��������=�ۼ�-���ۣ�
ʱ�����������������Ǿ������۴�������Ҫʹ�ڶ���������������650Ԫ��ʣ���T����ÿ���ۼ�����Ҫ����Ԫ��������=�ۼ�-���ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
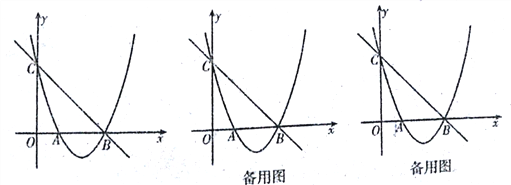
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���OΪ����ԭ�㣬������![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����B������Ϊ��3��0����ֱ��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����B������Ϊ��3��0����ֱ��![]() ����B��C���㣮
����B��C���㣮
��1���������ߵĽ���ʽ��
��2����P��x���·���������һ�㣬����AC������P��PQ��AC��BC�ڵ�Q������Q��x���ƽ���ߣ�����P��y���ƽ���ߣ�����ֱ���ཻ�ڵ�K��PK��BC�ڵ�H����QK�ij�Ϊt��PH�ij�Ϊd����d��t֮��ĺ�����ϵʽ������Ҫ��д���Ա���t��ȡֵ��Χ��
��3���ڣ�2���������£�PK��x���ڵ�R������R��RT��PQ������ΪT����PK=![]() PTʱ�����߶�QT�Ƶ�Q��ʱ����ת90
PTʱ�����߶�QT�Ƶ�Q��ʱ����ת90![]() �õ��߶�QL��M���߶�PQ��һ���㣬����M��ֱ��AC�Ĵ��ߣ�����ΪN������ON��ML����ML��ONʱ����N�����꣮
�õ��߶�QL��M���߶�PQ��һ���㣬����M��ֱ��AC�Ĵ��ߣ�����ΪN������ON��ML����ML��ONʱ����N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
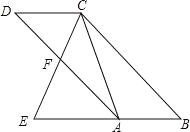
����Ŀ����ͼ����֪���ı���ABCD��ƽ���ı��Σ���E�ڱ�BA���ӳ����ϣ�CE��AD�ڵ�F����ECA=��D
��1����֤����EAC�ס�ECB��
��2����DF=AF����AC��BC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A�Ƿ���������![]() ��ͼ���ϵ�һ�����㣬����OA�������߶�OA�Ƶ�O˳ʱ����ת90��õ��߶�OB�����B����ͼ��ĺ�������ʽΪ________.
��ͼ���ϵ�һ�����㣬����OA�������߶�OA�Ƶ�O˳ʱ����ת90��õ��߶�OB�����B����ͼ��ĺ�������ʽΪ________.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com