
ĄūĖâÄŋĄŋÔÚÆ―ÃæÖą―ĮŨøąęÏĩÖÐĢŽĩãOΊŨøąęÔĩãĢŽÖąÏßy=Đ![]() x+12ÓëxÖáĢŽyÖá·ÖąðÏā―ŧÓÚĩãAĢŽBĢŽĄÏABOĩÄÆ―·ÖÏßÓëxÖáÏā―ŧÓÚĩãCĢŪ
x+12ÓëxÖáĢŽyÖá·ÖąðÏā―ŧÓÚĩãAĢŽBĢŽĄÏABOĩÄÆ―·ÖÏßÓëxÖáÏā―ŧÓÚĩãCĢŪ
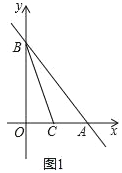
ĢĻ1ĢĐČįÍž1ĢŽĮóĩãCĩÄŨøąęĢŧ
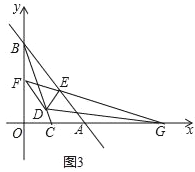
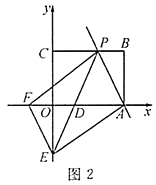
ĢĻ2ĢĐČįÍž2ĢŽĩãDĢŽEĢŽF·ÖąðÔÚÏßķÎBCĢŽABĢŽOBÉÏĢĻĩãDĢŽEĢŽFķžēŧÓëĩãBÖØšÏĢĐĢŽÁŽ―ÓDEĢŽDFĢŽEFĢŽĮŌĄÏEDF+ĄÏOBC=90ĄãĢŽĮóÖĪĢšĄÏFED=ĄÏAEDĢŧ
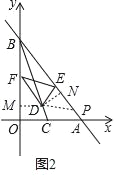
ĢĻ3ĢĐČįÍž3ĢŽÔÚĢĻ2ĢĐĩÄĖõžþÏÂĢŽŅÓģĪÏßķÎFEÓëxÖáÏā―ŧÓÚĩãGĢŽÁŽ―ÓDGĢŽČôĄÏCGD=ĄÏFGDĢŽBFĢšBE=5Ģš8ĢŽĮóÖąÏßDFĩÄ―âÎöĘ―ĢŪ

Ąūīð°ļĄŋĢĻ1ĢĐĩãCŨøąęΊĢĻ4ĢŽ0ĢĐĢŧĢĻ2ĢĐžû―âÎöĢŧĢĻ3ĢĐÖąÏßDFĩÄ―âÎöĘ―ÎŠy=Đ![]() x+7ĢŪ
x+7ĢŪ
Ąū―âÎöĄŋÕûĖå·ÖÎöĢš
ĢĻ1ĢĐŨũCHĄÍABÓÚHĢŽÓÉĄũOBCĄÕĄũHBCĮóBHĢŽ―âRtĄũACHĢŽĮóCHĢŽžīĩÃOCĢŧĢĻ2ĢĐđýĩãD·ÖąðŨũDMĄÍyÖáÓÚĩãMĢŽDNĄÍABÓÚĩãNĢŽÔÚNAÉÏ―ØČĄNP=FMĢŽÁŽ―ÓPDĢŽÓÃSASÖĪĄũDFMĄÕĄũDPNĢŽĩÃDF=DPĢŽĄÏEDF=ĄÏEDPĢŽÖĪĄũDEFĄÕĄũDEPĢŧĢĻ3ĢĐđýĩãFŨũFQĄÍBEÓÚĩãQĢŽđýĩãDŨũDMĄÍyÖáÓÚMĢŽDNĄÍABÓÚNĢŽDRĄÍEFÓÚRĢŽDSĄÍOGÓÚĩãSĢŽđýĩãAŨũATĄÍBC―ŧBCĩÄŅÓģĪÏßÓÚTĢŽÁŽ―ÓADĢŪ―âRtĄũACTĮóSTĢŽATĢŽĄÏADT=ĄÏDAT=45ĄãĢŽĮóDCĢŽīÓķøĩÃDSĢŽOSĢŽĮóģöDĩÄŨøąęĢŽÅÐķÏDFĄÎABĢŽžīŋÉĮóDFĩÄ―âÎöĘ―.
―âĢšĢĻ1ĢĐČįÍž1ĢŽŨũCHĄÍABÓÚHĢŪ

ÓÉĖâŌâAĢĻ9ĢŽ0ĢĐĢŽBĢĻ0ĢŽ12ĢĐĢŽ
ÔÚRtĄũAOBÖÐĢŽAB=![]() =
=![]() =15ĢŽtanĄÏOAB=
=15ĢŽtanĄÏOAB=![]() =
=![]() =
=![]() ĢŽ
ĢŽ
ĄßĄÏCBH=ĄÏCBOĢŽĄÏCHB=ĄÏCOBĢŽCB=CBĢŽ
ĄāĄũOBCĄÕĄũHBCĢŽ
ĄāBH=OB=12ĢŽOC=CHĢŽAH=15Đ12=3ĢŽ
ÔÚRtĄũACHÖÐĢŽtanĄÏCAH=![]() =
=![]() ĢŽ
ĢŽ
ĄÏCH=4ĢŽ
ĄāOC=CH=4ĢŽ
ĄāĩãCŨøąęΊĢĻ4ĢŽ0ĢĐĢŪ
ĢĻ2ĢĐ―âĢšČįÍž2ĢŽđýĩãD·ÖąðŨũDMĄÍyÖáÓÚĩãMĢŽDNĄÍABÓÚĩãNĢŽÔÚNAÉÏ―ØČĄNP=FMĢŽÁŽ―ÓPDĢŪ
ĄßĄÏEDF+ĄÏOBC=90ĄãĢŽĄÏBDM+ĄÏOBC=90ĄãĢŽ
ĄāĄÏEDF=ĄÏBDMĢŽÍŽĀíĄÏBDN=ĄÏBDM=![]() ĄÏMDNĢŽ
ĄÏMDNĢŽ
ĄāĄÏEDF=![]() ĄÏMDNĢŽ
ĄÏMDNĢŽ
ĄßĄÏDBM=ĄÏDBNĢŽDMĄÍOBĢŽDNĄÍABĢŽ
ĄāDM=DNĢŽ
ĄßĄÏFMD=ĄÏPND=90ĄãĢŽNP=FMĢŽ
ĄāĄũDFMĄÕĄũDPNĢŽ
ĄāDF=DPĢŽĄÏFDM=ĄÏPDNĢŽ
ĄāĄÏFDM+ĄÏFDN=ĄÏPDN+ĄÏFDNĢŽžīĄÏFDP=ĄÏMDNĢŽ
ĄāĄÏEDF=![]() ĄÏFDP=ĄÏEDPĢŽ
ĄÏFDP=ĄÏEDPĢŽ
ĄßDE=DEĢŽ
ĄāĄũDEFĄÕĄũDEPĢŽ
ĄāĄÏFED=ĄÏAEDĢŪ
ĢĻ3ĢĐ―âĢšČįÍž3ĢŽđýĩãFŨũFQĄÍBEÓÚĩãQĢŽđýĩãDŨũDMĄÍyÖáÓÚMĢŽDNĄÍABÓÚNĢŽDRĄÍEFÓÚRĢŽDSĄÍOGÓÚĩãSĢŽđýĩãAŨũATĄÍBC―ŧBCĩÄŅÓģĪÏßÓÚTĢŽÁŽ―ÓADĢŪ
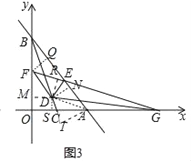
ĄßĄÏDEF=ĄÏDEAĢŽDRĄÍEFĢŽDNĄÍEAĢŽ
ĄāDR=DNĢŽÍŽĀíDR=DSĢŽ
ĄāDN=DSĢŽ
ĄāĄÏBAD=ĄÏOADĢŽÍŽĀíĄÏOFD=ĄÏDFGĢŽ
ÔÚRtĄũACTÖÐĢŽAC=9Đ4=5ĢŽtanĄÏACT=tanĄÏBCO=![]() =3ĢŽ
=3ĢŽ ![]() =3ĢŽ
=3ĢŽ
ÉčCT=mĢŽÔōAT=3mĢŪ
ĄßCT2+AT2=AC2ĢŽ
Ąām2+ĢĻ3mĢĐ2=52ĢŽ
―âĩÃm=![]() ŧōĐ
ŧōĐ![]() ĢĻÉáĢĐĢŽ
ĢĻÉáĢĐĢŽ
ĄāCT=![]() ĢŽAT=
ĢŽAT=![]() ĢŽ
ĢŽ
ĄßĄÏADC=ĄÏABD+ĄÏBAD=![]() ĢĻĄÏOBA+ĄÏBAOĢĐ=
ĢĻĄÏOBA+ĄÏBAOĢĐ=![]() ĄÁ90Ąã=45ĄãĢŽ
ĄÁ90Ąã=45ĄãĢŽ
ĄāĄÏDAT=45Ąã=ĄÏADCĢŽ
ĄāDT=AT=![]() ĢŽ
ĢŽ
ĄāCD=DTĐCT=![]() ĢŽÍŽĀíŋÉĩÃĢŽCS=1ĢŽDS=3=OMĢŽ
ĢŽÍŽĀíŋÉĩÃĢŽCS=1ĢŽDS=3=OMĢŽ
ĄāOS=4Đ1=3ĢŽ
ĄāĩãDŨøąęĢĻ3ĢŽ3ĢĐĢŽ
ÉčBF=5nĢŽÔōBE=8nĢŽÔÚRtĄũBFQÖÐĢŽcosĄÏFBQ=![]() =
=![]() =
=![]() ĢŽ
ĢŽ
ĄāBQ=4n=EQĢŽ
ĄāFQĄÍABĢŽĄÏBFQ=ĄÏEFQĢŽ
ĄāĄÏDFQ=ĄÏDFC+ĄÏEFQ=![]() ĢĻĄÏOFG+ĄÏBFEĢĐ=
ĢĻĄÏOFG+ĄÏBFEĢĐ=![]() ĄÁ180Ąã=90ĄãĢŽ
ĄÁ180Ąã=90ĄãĢŽ
ĄāĄÏDFQ=ĄÏBQF=90ĄãĢŽ
ĄāDFĄÎABĢŽ
ÉčÖąÏßDFĩÄ―âÎöĘ―ÎŠy=Đ![]() x+bĢŽ
x+bĢŽ
Ąā3=Đ![]() ĄÁ3+bĢŽ
ĄÁ3+bĢŽ
―âĩÃb=7ĢŽ
ĄāÖąÏßDFĩÄ―âÎöĘ―ÎŠy=Đ![]() x+7ĢŪ
x+7ĢŪ


 ÍõšóÐÛŅ§°ļ―ĖēÄÍęČŦ―âķÁÏĩÁÐīð°ļ
ÍõšóÐÛŅ§°ļ―ĖēÄÍęČŦ―âķÁÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽūØÐÎ![]() °Ú·ÅÔÚÆ―ÃæÖą―ĮŨøąęÏĩÖÐĢŽĩã
°Ú·ÅÔÚÆ―ÃæÖą―ĮŨøąęÏĩÖÐĢŽĩã![]() ÔÚ
ÔÚ![]() ÖáÉÏĢŽĩã
ÖáÉÏĢŽĩã![]() ÔÚ
ÔÚ![]() ÖáÉÏĢŽ
ÖáÉÏĢŽ
![]() ĢŽ
ĢŽ![]() ĢŽđýĩã
ĢŽđýĩã![]() ĩÄÖąÏß―ŧūØÐÎ
ĩÄÖąÏß―ŧūØÐÎ![]() ĩÄąß
ĩÄąß![]() ÓÚĩã
ÓÚĩã![]() ĢŽĮŌĩã
ĢŽĮŌĩã![]() ēŧÓëĩã
ēŧÓëĩã![]() ĄĒ
ĄĒ![]() ÖØšÏĢŽđýĩã
ÖØšÏĢŽđýĩã![]() Ũũ
Ũũ![]() ĢŽ
ĢŽ![]() ―ŧ
―ŧ![]() ÖáÓÚĩã
ÖáÓÚĩã![]() ĢŽ―ŧ
ĢŽ―ŧ![]() ÖáÓÚĩã
ÖáÓÚĩã![]() .
.
ĢĻ1ĢĐČįÍž1ĢŽČô![]() ΊĩČŅüÖą―ĮČý―ĮÐÎĢŽĮóÖąÏß
ΊĩČŅüÖą―ĮČý―ĮÐÎĢŽĮóÖąÏß![]() ĩÄšŊĘý―âÎöĘ―Ģŧ
ĩÄšŊĘý―âÎöĘ―Ģŧ
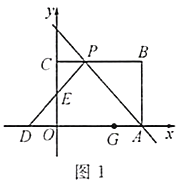
ĢĻ2ĢĐČįÍž2ĢŽđýĩã![]() Ũũ
Ũũ![]() ―ŧ
―ŧ![]() ÖáÓÚĩã
ÖáÓÚĩã![]() ĢŽČôËÄąßÐÎ
ĢŽČôËÄąßÐÎ![]() ĘĮÆ―ÐÐËÄąßÐÎĢŽĮóÖąÏß
ĘĮÆ―ÐÐËÄąßÐÎĢŽĮóÖąÏß![]() ĩÄ―âÎöĘ―.
ĩÄ―âÎöĘ―.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚÖą―ĮŨøąęÏĩÖÐĢŽÕý·―ÐÎOABCĩÄķĨĩãOÓëÔĩãÖØšÏĢŽķĨĩãAĢŽC·ÖąðÔÚxÖáĢŽyÖáÉÏĢŽ·īąČĀýšŊĘýĩÄÍžÏóÓëÕý·―ÐÎĩÄÁ―ąßABĢŽBC·Öąð―ŧÓÚĩãMĢŽNĢŽNDĄÍxÖáĢŽīđŨãΊDĢŽÁŽ―ÓOMĢŽONĢŽMN.ÏÂÁÐ―áÂÛĢšĒŲĄũOCNĄÕĄũOAMĢŧĒÚONĢ―MNĢŧĒÛËÄąßÐÎDAMNÓëĄũMONÃæŧýÏāĩČĢŧĒÜČôĄÏMONĢ―45ĄãĢŽMNĢ―2ĢŽÔōĩãCĩÄŨøąęΊ(0ĢŽ ![]() ĢŦ1)ĢŪÆäÖÐÕýČ·―áÂÛĩÄÐōšÅĘĮ____________ĢŪ
ĢŦ1)ĢŪÆäÖÐÕýČ·―áÂÛĩÄÐōšÅĘĮ____________ĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
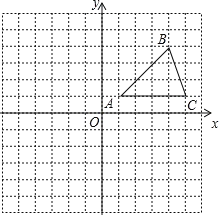
ĄūĖâÄŋĄŋÔÚÆ―ÃæÖą―ĮŨøąęÏĩÖÐĢŽĄũABCĩÄÎŧÖÃČįÍžËųĘū(ÃŋļöÐĄ·―ļņķžĘĮąßģĪΊ1ļöĩĨÎŧģĪķČĩÄÕý·―ÐÎ)ĄĢ
(1)―ŦĄũABCŅØxÖá·―ÏōÏōŨóÆ―ŌÆ6ļöĩĨÎŧĢŽŧģöÆ―ŌÆšóĩÃĩ―ĩÄĄũA1B1C1
(2)―ŦĄũABCČÆŨÅĩãAËģĘąÕëÐýŨŠ90ĄãĢŽŧģöÐýŨŠšóĩÃĩ―ĩÄĄũAB2C2ĢŽēĒÖą―ÓÐīģöĩãB2ĄĒC2ĩÄŨøąęĢŧ
(3)ÔÚĩÚ(2)ÎĘÖÐĢŽĩãBÐýŨŠĩ―ĩãB2ĩÄđýģĖÖÐÔËķŊĩÄ·ūķģĪĘĮ_____.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÎĘĖâĮéĖîĢŽ
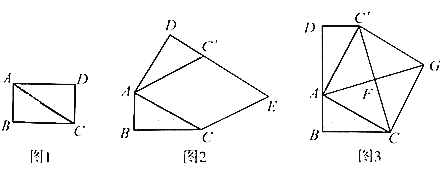
ÔÚŨÛšÏÓëĘĩžųŋÎÉÏĢŽĀÏĘĶČÃÍŽŅ§ÃĮŌÔĄ°ūØÐÎÖ―ÆŽĩÄžôÆīĄąÎŠÖũĖâŋŠÕđĘýŅ§ŧîķŊĢŽČįÍž1ĢŽ―ŦūØÐÎÖ―ÆŽABCDŅØķÔ―ĮÏßACžôŋŠĢŽĩÃĩ―ĄũABCšÍĄũACDĄĒēĒĮŌÁŋĩÃABĢ―2cmĢŽACĢ―4cm.
ēŲŨũ·ĒÏÖĢš
(1)―ŦÍž1ÖÐĩÄĄũACDŌÔĩãAΊÐýŨŠÖÐÐÄĢŽ°īÄæĘąÕë·―ÏōÐýŨŠĄÏĶÁĢŽĘđĄÏĶÁĢ―ĄÏBACĢŽĩÃĩ―žÓÍž2ËųĘūĩÄĄũACĄäDĢŽđýĩãCŨũACĄäĩÄÆ―ÐÐÏßĢŽÓëDCĄäĩÄŅÓģĪÏß―ŧÓÚĩãEĢŽÔōËÄąßÐÎACEC'ĩÄÐÎŨīĘĮ_________Ģŧ
(2)īīÐÂÐĄŨé―ŦÍž1ÖÐĩÄĄũACDŌÔĩãAΊÐýŨŠÖÐÐÄĢŽ°īÄæĘąÕë·―ÏōÐýŨŠĢŽĘđBĢŽAĢŽDČýĩãÔÚÍŽŌŧĖõÖąÏßÉÏĢŽĩÃĩ―ČįÍž3ËųĘūĩÄĄũACĄäDĢŽÁŽ―ÓCCĄäĢŽČĄCC'ĩÄÖÐĩãFĢŽÁŽūŦAFēĒŅÓģĪĩ―ĩãGĢŽĘđFGĢ―AFĢŽÁŽ―ÓCGĢŽCĄäGĢŽĩÃĩ―ËÄąßÐÎACGCĄäĢŽ·ĒÏÖËüĘĮÕý·―ÐÎĢŽĮëÄãÖĪÃũÕâļö―áÂÛ.
ĘĩžųĖ―ūŋĢš
(3)įĮÃÜÐĄŨéÔÚīīÐÂÐĄŨé·ĒÏÖ―áÂÛĩÄŧųīĄÉÏĢŽ―øÐÐČįÏÂēŲŨũĢš―ŦĄũABCŅØŨÅBD·―ÏōÆ―ŌÆĢŽĘđĩãBÓëĩãAÖØšÏĢŽīËĘąAĩãÆ―ŌÆÖÁAĄäĩãĢŽAĄäCÓëBCĄäÏā―ŧÓÚĩãH.ČįÍž4ËųĘūĢŽÁŽ―ÓCC'ĢŽĘÔĮóCHĩÄģĪķČ.
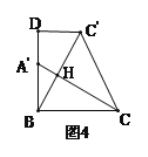
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠRtĄũABCÖÐĢŽĄÏCĢ―90ĄãĢŪ
ĢĻ1ĢĐŌŅÖŠ aĢ―4![]() ĢŽ bĢ―2
ĢŽ bĢ―2![]() ĢŽĮó c Ģŧ
ĢŽĮó c Ģŧ
ĢĻ2ĢĐŌŅÖŠĄÏAĢ―60ĄãĢŽ cĢ―2![]() ĢŦ4ĢŽĮó b Ģŧ
ĢŦ4ĢŽĮó b Ģŧ
ĢĻ3ĢĐŌŅÖŠ a Ģ―10ĢŽ c Ģ―10![]() ĢŽĮóĄÏBĢŧ
ĢŽĮóĄÏBĢŧ
ĢĻ4ĢĐŌŅÖŠ b Ģ―35ĢŽĄÏAĢ―45ĄãĢŽĮó a ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽĄõABCDĩÄķÔ―ĮÏßACĄĒBDÏā―ŧÓÚĩãOĢŽAEĢ―CFĢŪ
ĢĻ1ĢĐĮóÖĪĢšĄũBOEĄÕĄũDOFĢŧ
ĢĻ2ĢĐČôBDĢ―EFĢŽÁŽ―ÓDEĄĒBFĢŽÅÐķÏËÄąßÐÎEBFDĩÄÐÎŨīĢŽēĒËĩÃũĀíÓÉĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
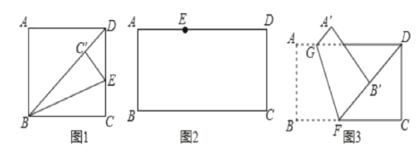
ĄūĖâÄŋĄŋ(1)ČįÍž1ĢŽ―ŦūØÐÎABCDÕÛĩþĢŽĘđBCÂäÔÚķÔ―ĮÏßBDÉÏĢŽÕÛšÛΊBEĢŽĩãCÂäÔÚĩãC'īĶĢŽČôĄÏADB=46ĄãĢŽÔōĄÏDBEĩÄķČĘýΊ______.
(2)ÐĄÃũĘÖÖÐÓÐŌŧÕÅūØÐÎÖ―ÆŽABCDĢŽAB=4ĢŽAD=9ĢŪ
ĢĻŧŌŧŧĢĐ
ČįÍž2ĢŽĩãEÔÚÕâÕÅūØÐÎÖ―ÆŽĩÄąßADÉÏĢŽ―ŦÖ―ÆŽÕÛĩþĢŽĘđABÂäÔÚCEËųÔÚÖąÏßÉÏĢŽÕÛšÛÉčΊMN(ĩãMĢŽN·ÖąðÔÚąßADĢŽBCÉÏ)ĢŽĀûÓÃÖąģßšÍÔēđæŧģöÕÛšÛMN(ēŧÐīŨũ·ĻĢŽąĢÁôŨũÍžšÛžĢĢŽēĒÓÚÚÉŦËŪąĘ°ŅÏßķÎÃčĮåģþ)Ģŧ
ĢĻËãŌŧËãĢĐ
ČįÍž3ĢŽĩãFÔÚÕâÕÅūØÐÎÖ―ÆŽĩÄąßBCÉÏĢŽ―ŦÖ―ÆŽÕÛĩþĢŽĘđFBÂäÔÚÉäÏßFDÉÏĢŽÕÛšÛΊGFĢŽĩãAĢŽB·ÖąðÂäÔÚĩãA'ĢŽB'īĶĢŽČôAG=![]() ĢŽĮóB'DĩÄģĪĢŧ
ĢŽĮóB'DĩÄģĪĢŧ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
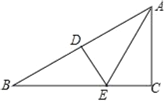
ĄūĖâÄŋĄŋČįÍžĢŽÔÚĄũABCÖÐĢŽĄÏBĢ―30ĄãĢŽąßABĩÄīđÖąÆ―·ÖÏß·Öąð―ŧABšÍBCÓÚĩãDĢŽEĢŽĮŌAEÆ―·ÖĄÏBACĢŪ
ĢĻ1ĢĐĮóĄÏCĩÄķČĘýĢŧ
ĢĻ2ĢĐČôCEĢ―1ĢŽĮóABĩÄģĪĢŪ
ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com