
【题目】如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴,y轴上,反比例函数的图象与正方形的两边AB,BC分别交于点M,N,ND⊥x轴,垂足为D,连接OM,ON,MN.下列结论:①△OCN≌△OAM;②ON=MN;③四边形DAMN与△MON面积相等;④若∠MON=45°,MN=2,则点C的坐标为(0, ![]() +1).其中正确结论的序号是____________.
+1).其中正确结论的序号是____________.

【答案】①③④
【解析】试题解析:设反比例函数的解析式为: ![]()
∵点M、N都在![]() 的图象上,
的图象上,
∴![]() 即
即![]()
∵四边形ABCO为正方形,
∴![]()
∴NC=AM,
∴△OCN≌△OAM, ∴①正确;
∵△OCN≌△OAM,∴ON=OM,
∵k的值不能确定,
∴∠MON的值不能确定,
∴△ONM只能为等腰三角形,不能确定为等边三角形,
∴ON≠MN,
∴②错误;
∵![]()
而S△OND+S四边形DAMN=S△OAM+S△OMN,
∴四边形DAMN与△MON面积相等,
∴③正确;
作NE⊥OM于E点,如图所示:
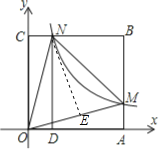
∵![]() ,∴△ONE为等腰直角三角形,
,∴△ONE为等腰直角三角形,
∴NE=OE,
设NE=x,则![]()
∴![]()
∴![]()
在Rt△NEM中,MN=2,
∵![]() 即
即![]()
∴![]()
∴![]()
∵CN=AM,CB=AB,
∴BN=BM,
∴△BMN为等腰直角三角形,
∴![]()
设正方形ABCO的边长为a,则![]()
在Rt△OCN中, ![]()
∴![]() 解得
解得![]() (舍去),
(舍去),
∴![]()
∴C点坐标为![]()
∴④正确.
故答案为:①③④.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】下列图形都是由相同的小正方形按照一定规律摆放而成,其中第1个图共有3个小正方形,第2个图共有8个小正方形,第3个图共有15个小正方形,第4个图共有24个小正方形,…,照此规律排列下去,则第8个图中小正方形的个数是( )
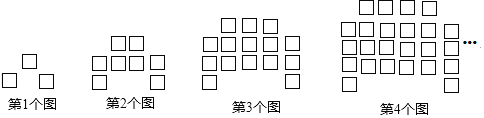
A. 48B. 63C. 80D. 99
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() (0,1),点
(0,1),点![]() (1,0),正方形
(1,0),正方形![]() 的两条对角线的交点为
的两条对角线的交点为![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() .延长
.延长![]() 至点
至点![]() ,使
,使![]() ,以
,以![]() ,
,![]() 为邻边做正方形
为邻边做正方形![]() .
.
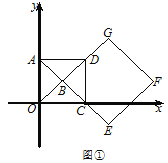
(Ⅰ)如图①,求![]() 的长及
的长及![]() 的值;
的值;
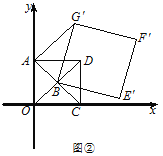
(Ⅱ)如图②,正方形![]() 固定,将正方形
固定,将正方形![]() 绕点
绕点![]() 逆时针旋转,得正方形
逆时针旋转,得正方形![]() ,记旋转角为
,记旋转角为![]() (0°<
(0°<![]() <360°),连接
<360°),连接![]() .
.
①旋转过程中,当![]() 90°时,求
90°时,求![]() 的大小;
的大小;
②在旋转过程中,求![]() 的长取最大值时,点
的长取最大值时,点![]() 的坐标及此时
的坐标及此时![]() 的大小(直接写出结果即可).
的大小(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(Ⅰ)若抛物线的顶点为![]() (-2,-4),抛物线经过点
(-2,-4),抛物线经过点![]() (-4,0).
(-4,0).
①求该抛物线的解析式;
②连接![]() ,把
,把![]() 所在直线沿
所在直线沿![]() 轴向上平移,使它经过原点
轴向上平移,使它经过原点![]() ,得到直线
,得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一动点.
上一动点.
设以点![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形的面积为
为顶点的四边形的面积为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() ≤
≤![]() ≤
≤![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() >0,
>0, ![]() >1,当
>1,当![]() 时,
时, ![]() ,当0<
,当0<![]() <
<![]() 时,
时, ![]() >0,试比较
>0,试比较![]() 与1的大小,并说明理由.
与1的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是对角线AC上一点(不与点A、C重合),连接PD,过点P作PE⊥PD交射线BC于点E.
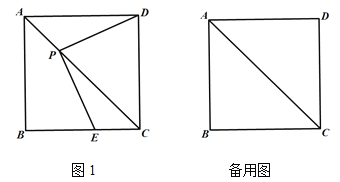
(1)如图1,求证:PD=PE;
(2)若正方形ABCD的边长为4,![]() ,求CE长.
,求CE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
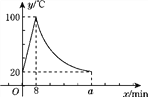
【题目】教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10 ℃,待加热到100 ℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20 ℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40 ℃的开水,则他需要在什么时间段内接水?
查看答案和解析>>
科目:初中数学 来源: 题型:
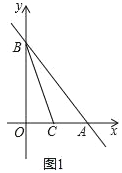
【题目】在平面直角坐标系中,点O为坐标原点,直线y=﹣![]() x+12与x轴,y轴分别相交于点A,B,∠ABO的平分线与x轴相交于点C.
x+12与x轴,y轴分别相交于点A,B,∠ABO的平分线与x轴相交于点C.
(1)如图1,求点C的坐标;
(2)如图2,点D,E,F分别在线段BC,AB,OB上(点D,E,F都不与点B重合),连接DE,DF,EF,且∠EDF+∠OBC=90°,求证:∠FED=∠AED;
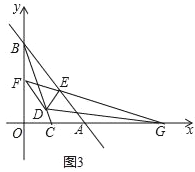
(3)如图3,在(2)的条件下,延长线段FE与x轴相交于点G,连接DG,若∠CGD=∠FGD,BF:BE=5:8,求直线DF的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
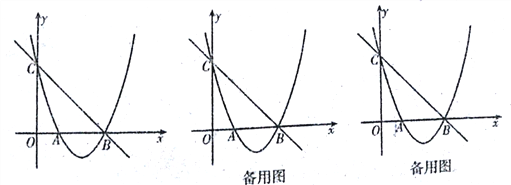
【题目】如图,在平面直角坐标系xOy中,点O为坐标原点,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),直线
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),直线![]() 经过B、C两点.
经过B、C两点.
(1)求抛物线的解析式;
(2)点P是x轴下方抛物线上一点,连接AC,过点P作PQ∥AC交BC于点Q,过点Q作x轴的平行线,过点P作y轴的平行线,两条直线相交于点K,PK交BC于点H,设QK的长为t,PH的长为d,求d与t之间的函数关系式;(不要求写出自变量t的取值范围)
(3)在(2)的条件下,PK交x轴于点R,过点R作RT⊥PQ,垂足为T,当PK=![]() PT时,将线段QT绕点Q逆时针旋转90
PT时,将线段QT绕点Q逆时针旋转90![]() 得到线段QL,M是线段PQ上一动点,过点M作直线AC的垂线,垂足为N,连接ON、ML,当ML∥ON时,求N点坐标.
得到线段QL,M是线段PQ上一动点,过点M作直线AC的垂线,垂足为N,连接ON、ML,当ML∥ON时,求N点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com