
【题目】已知抛物线![]() .
.
(Ⅰ)若抛物线的顶点为![]() (-2,-4),抛物线经过点
(-2,-4),抛物线经过点![]() (-4,0).
(-4,0).
①求该抛物线的解析式;
②连接![]() ,把
,把![]() 所在直线沿
所在直线沿![]() 轴向上平移,使它经过原点
轴向上平移,使它经过原点![]() ,得到直线
,得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一动点.
上一动点.
设以点![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形的面积为
为顶点的四边形的面积为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() ≤
≤![]() ≤
≤![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() >0,
>0, ![]() >1,当
>1,当![]() 时,
时, ![]() ,当0<
,当0<![]() <
<![]() 时,
时, ![]() >0,试比较
>0,试比较![]() 与1的大小,并说明理由.
与1的大小,并说明理由.
【答案】(Ⅰ)①该抛物线的解析式为![]() ;②当点
;②当点![]() 在第二象限时,
在第二象限时, ![]() <0,
<0, ![]() 的取值范围是
的取值范围是![]() ≤
≤![]() ≤
≤![]() ,当点
,当点![]() 在第四象限时,
在第四象限时, ![]() >0,
>0,
![]() 的取值范围是
的取值范围是![]() ≤
≤![]() ≤
≤![]() ;(Ⅱ)
;(Ⅱ)![]() ≤1.
≤1.
【解析】试题分析:(Ⅰ)①用顶点式即可求出抛物线的解析式;
②首先可以得出直线AB和直线l的解析式.然后分两种情况讨论:①当P在第二象限时,②当P在第四象限时.
(Ⅱ)由当![]() 时,
时, ![]() ,得到
,得到![]() .由
.由![]() 时,
时, ![]() ,知抛物线与
,知抛物线与![]() 轴的一个公共点为(
轴的一个公共点为(![]() ,0).由0<
,0).由0<![]() <
<![]() 时,
时, ![]() >0,知抛物线的对称轴
>0,知抛物线的对称轴![]() ≥
≥![]() ,从而得到
,从而得到 ![]() ≤
≤![]() ,即可得到结论.
,即可得到结论.
试题解析:解:(Ⅰ)①设抛物线的解析式为![]() .
.
∵抛物线经过点![]() (-4,0),∴
(-4,0),∴![]() .解得:
.解得: ![]() ,∴
,∴![]() ,∴该抛物线的解析式为
,∴该抛物线的解析式为![]() .
.
②设直线![]() 的解析式为
的解析式为![]() ,由
,由![]() (-2,-4),
(-2,-4),![]() (-4,0),得:
(-4,0),得: ![]() ,解这个方程组,得:
,解这个方程组,得: ![]() ,∴直线
,∴直线![]() 的解析式为
的解析式为![]() .
.
∵直线![]() 与
与![]() 平行,且过原点,∴直线
平行,且过原点,∴直线![]() 的解析式为
的解析式为![]() .
.
当点![]() 在第二象限时,
在第二象限时, ![]() <0,如图,
<0,如图,
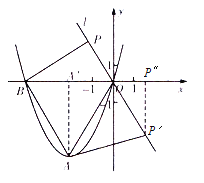
![]() .
. ![]() ,∴
,∴![]() (
(![]() <0).
<0).
∵![]() ≤
≤![]() ≤
≤![]() ,∴
,∴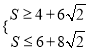 ,即
,即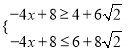 ,
,
解此不等式组,得: ![]() ≤
≤![]() ≤
≤![]() .
.
∴![]() 的取值范围是
的取值范围是![]() ≤
≤![]() ≤
≤![]() .
.
当点![]() 在第四象限时,
在第四象限时, ![]() >0,过点
>0,过点![]() ,
, ![]() 分别作
分别作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
, ![]() ,则:
,则:
![]() ·
·![]() ·
·![]() ·
·![]() .
.
∵![]() ,∴
,∴![]() (
(![]() >0).
>0).
∵![]() ≤
≤![]() ≤
≤![]() ,∴
,∴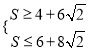 ,即
,即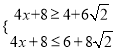 ,
,
解此不等式组,得: ![]() ≤
≤![]() ≤
≤![]() .
.
∴![]() 的取值范围是
的取值范围是![]() ≤
≤![]() ≤
≤![]() .
.
(Ⅱ)∵当![]() 时,
时, ![]() ,∴
,∴![]() .
.
∵![]() >1,∴
>1,∴![]() ,
, ![]() .
.
由![]() 时,
时, ![]() ,知抛物线与
,知抛物线与![]() 轴的一个公共点为(
轴的一个公共点为(![]() ,0).
,0).
把![]() 代入
代入![]() ,得:
,得: ![]() ,∴抛物线与
,∴抛物线与![]() 轴的交点为(0,
轴的交点为(0, ![]() ).
).
由![]() >0知抛物线开口向上,再由0<
>0知抛物线开口向上,再由0<![]() <
<![]() 时,
时, ![]() >0,知抛物线的对称轴
>0,知抛物线的对称轴![]() ≥
≥![]() ,∴
,∴![]() ≤
≤![]() .由
.由![]() 得:
得: ![]() ≤
≤![]() ,∴
,∴![]() ≤1.
≤1.


科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂加工某种茶叶,计划一周生产![]() 千克,平均每天生产
千克,平均每天生产![]() 千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(![]() )这一周的实际产量是多少千克?
)这一周的实际产量是多少千克?
(![]() )该厂规定工人工资参照平均产量计发,每千克
)该厂规定工人工资参照平均产量计发,每千克![]() 元.若超产,则超产的部分每千克
元.若超产,则超产的部分每千克![]() 元;若低于平均产量,按实际产量计发,而且每少
元;若低于平均产量,按实际产量计发,而且每少![]() 千克扣除
千克扣除![]() 元,那么该工厂工人这一周的工资总额是多少?
元,那么该工厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减(辆) | -1 | +3 | -2 | -4 | +7 | -5 | -10 |
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC的延长线于点F.
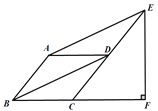
(1)求证:四边形ABCD是菱形;(2)若∠ABC=45°,BC=1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴,y轴上,反比例函数的图象与正方形的两边AB,BC分别交于点M,N,ND⊥x轴,垂足为D,连接OM,ON,MN.下列结论:①△OCN≌△OAM;②ON=MN;③四边形DAMN与△MON面积相等;④若∠MON=45°,MN=2,则点C的坐标为(0, ![]() +1).其中正确结论的序号是____________.
+1).其中正确结论的序号是____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
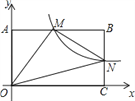
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=–![]() x+3交AB,BC于点M,N,反比例函数
x+3交AB,BC于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情填,
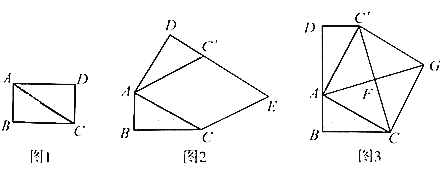
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动,如图1,将矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD、并且量得AB=2cm,AC=4cm.
操作发现:
(1)将图1中的△ACD以点A为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到加图2所示的△AC′D,过点C作AC′的平行线,与DC′的延长线交于点E,则四边形ACEC'的形状是_________;
(2)创新小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B,A,D三点在同一条直线上,得到如图3所示的△AC′D,连接CC′,取CC'的中点F,连精AF并延长到点G,使FG=AF,连接CG,C′G,得到四边形ACGC′,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至A′点,A′C与BC′相交于点H.如图4所示,连接CC',试求CH的长度.
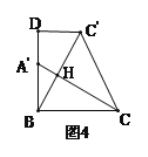
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A. C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y=![]() (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,
(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,![]() ).
).
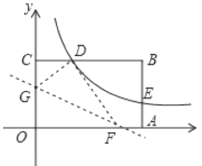
(1)求反比例函数的表达式和m的值;
(2)将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com