
【题目】如图,矩形OABC的顶点A. C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y=![]() (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,
(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,![]() ).
).
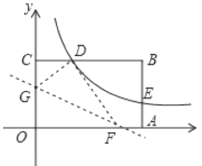
(1)求反比例函数的表达式和m的值;
(2)将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式。
【答案】(1)y=![]() ,m=1(2)y=
,m=1(2)y=![]() x+
x+![]()
【解析】
(1)由点E的坐标利用反比例函数图象上点的坐标特征即可求出k值,再由点B在反比例函数图象上,代入即可求出m值;
(2)设OG=x,利用勾股定理即可得出关于x的一元二次方程,解方程即可求出x值,从而得出点G的坐标.再过点F作FH⊥CB于点H,由此可得出△GCD∽△DHF,根据相似三角形的性质即可求出线段DF的长度,从而得出点F的坐标,结合点G、F的坐标利用待定系数法即可求出结论.
(1)∵反比例函数y=kx(k≠0)在第一象限内的图象经过点E(3, ![]() ),
),
∴k=3×![]() =2,
=2,
∴反比例函数的表达式为y=![]() .
.
又∵点D(m,2)在反比例函数y=![]() 的图象上,
的图象上,
∴2m=2,解得:m=1.
(2)设OG=x,则CG=OCOG=2x,
∵点D(1,2),
∴CD=1.
在Rt△CDG中,∠DCG=90°,CG=2x,CD=1,DG=OG=x,
∴CD![]() +CG
+CG![]() =DG
=DG![]() ,即1+(2x)
,即1+(2x)![]() =x
=x![]() ,
,
解得:x=![]() ,
,
∴点G(0, ![]() ).
).
过点F作FH⊥CB于点H,如图所示。
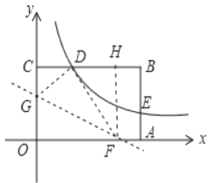
由折叠的特性可知:∠GDF=∠GOF=90°,OG=DG,OF=DF.
∵∠CGD+∠CDG=90°,∠CDG+∠HDF=90°,
∴∠CGD=∠HDF,
∵∠DCG=∠FHD=90°,
∴△GCD∽△DHF,
∴![]() ,
,
∴DF=2GD=![]() ,
,
∴点F的坐标为(![]() ,0).
,0).
设折痕FG所在直线的函数关系式为y=ax+,
∴有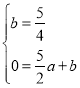 ,解得:
,解得: .
.
∴折痕FG所在直线的函数关系式为y=![]() x+
x+![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(Ⅰ)若抛物线的顶点为![]() (-2,-4),抛物线经过点
(-2,-4),抛物线经过点![]() (-4,0).
(-4,0).
①求该抛物线的解析式;
②连接![]() ,把
,把![]() 所在直线沿
所在直线沿![]() 轴向上平移,使它经过原点
轴向上平移,使它经过原点![]() ,得到直线
,得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一动点.
上一动点.
设以点![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形的面积为
为顶点的四边形的面积为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() ≤
≤![]() ≤
≤![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() >0,
>0, ![]() >1,当
>1,当![]() 时,
时, ![]() ,当0<
,当0<![]() <
<![]() 时,
时, ![]() >0,试比较
>0,试比较![]() 与1的大小,并说明理由.
与1的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某省将地处A,B两地的两所大学合并成了一所综合性大学.为了方便A,B两地师生交往,学校准备在相距 2千米 的A,B两地之间修筑一条笔直的公路(即图4.33中的线段AB).经测量,在A地的北偏东60°方向,B地北偏西45°方向的C处有一个半径为0.7千米的公园,问计划修筑的这条公路会不会穿过公园 为什么
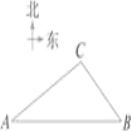
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下来往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟后妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法中错误的是( )

A. 打电话时,小刚和妈妈的距离为1250米
B. 打完电话后,经过23分钟小刚到达学校
C. 小刚和妈妈相遇后,妈妈回家的速度为150米/分
D. 小刚家与学校的距离为2550米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC∥GE,AF∥DE,∠1=50°.
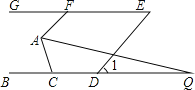
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
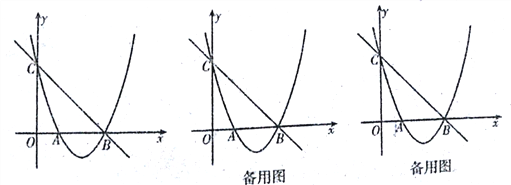
【题目】如图,在平面直角坐标系xOy中,点O为坐标原点,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),直线
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),直线![]() 经过B、C两点.
经过B、C两点.
(1)求抛物线的解析式;
(2)点P是x轴下方抛物线上一点,连接AC,过点P作PQ∥AC交BC于点Q,过点Q作x轴的平行线,过点P作y轴的平行线,两条直线相交于点K,PK交BC于点H,设QK的长为t,PH的长为d,求d与t之间的函数关系式;(不要求写出自变量t的取值范围)
(3)在(2)的条件下,PK交x轴于点R,过点R作RT⊥PQ,垂足为T,当PK=![]() PT时,将线段QT绕点Q逆时针旋转90
PT时,将线段QT绕点Q逆时针旋转90![]() 得到线段QL,M是线段PQ上一动点,过点M作直线AC的垂线,垂足为N,连接ON、ML,当ML∥ON时,求N点坐标.
得到线段QL,M是线段PQ上一动点,过点M作直线AC的垂线,垂足为N,连接ON、ML,当ML∥ON时,求N点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商从市场得知如下信息:
A品牌计算器 | B品牌计算器 | |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他计划用不超过4万元的资金一次性购进这两种品牌计算器共100台,设该经销商购进A品牌计算器x台,这两种品牌计算器全部销售完后获得利润为y元.
(1)求y与x之间的函数关系式;
(2)若要求全部销售完后获得的利润不少于1.26万元,该经销商有哪几种进货方案?
(3)选择哪种进货方案,该经销商可获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
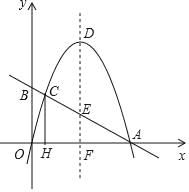
【题目】如图,二次函数y=﹣x2+bx的图象与x轴的正半轴交于点A(4,0),过A点的直线与y轴的正半轴交于点B,与二次函数的图象交于另一点C,过点C作CH⊥x轴,垂足为H.设二次函数图象的顶点为D,其对称轴与直线AB及x轴分别交于点E和点F.
(1)求这个二次函数的解析式;
(2)如果CE=3BC,求点B的坐标;
(3)如果△DHE是以DH为底边的等腰三角形,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
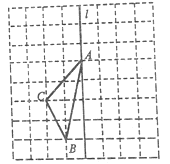
【题目】如图,由边长均为1个单位的小正方形组成的网格图中,点![]() 都在格点上。
都在格点上。
(1)![]() 的面积为__________________________;
的面积为__________________________;
(2)以![]() 为边画出一个与
为边画出一个与![]() 全等的三角形,并进一步探究:满足条件的三角形可以作出_____;
全等的三角形,并进一步探究:满足条件的三角形可以作出_____;
(3)在直线![]() 上确定点
上确定点![]() ,使
,使![]() 的长度最短.(画出示意图,并标明点
的长度最短.(画出示意图,并标明点![]() 的位置即可)
的位置即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com