
【题目】如图,二次函数y=﹣x2+bx的图象与x轴的正半轴交于点A(4,0),过A点的直线与y轴的正半轴交于点B,与二次函数的图象交于另一点C,过点C作CH⊥x轴,垂足为H.设二次函数图象的顶点为D,其对称轴与直线AB及x轴分别交于点E和点F.
(1)求这个二次函数的解析式;
(2)如果CE=3BC,求点B的坐标;
(3)如果△DHE是以DH为底边的等腰三角形,求点E的坐标.
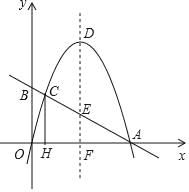
【答案】(1)y=﹣x2+4x;(2)B(0,2);(3)E(2,﹣12+8![]() )
)
【解析】整体分析:
(1)把A(4,0)代入抛物线y=﹣x2+bx即可求b;(2)由抛物线的性质求OF,AF的长,根据平行线分线段成比例定理,及CE=3BC,求OH,则可得CH,由△ACH∽△ABC求OB;(3)设点C的坐标为(x,﹣x2+4x),由△ACH∽△AEF,用x表示点E的坐标,根据ED=EH,用勾股定理列方程求解.
解:(1)∵抛物线y=﹣x2+bx经过点A(4,0),
∴﹣16+4b=0,∴b=4,
∴y=﹣x2+4x,
∴抛物线的解析式为y=﹣x2+4x;
(2)∵y=﹣(x﹣2)2+4,顶点D的坐标是(2,4),∴OF=AF=2,
∵BO∥CH∥EF,∴![]() =
=![]()
∵CE=3BC,∴![]() =
=![]() ,
,
∴OH=![]() ,∴CH=y﹣(
,∴CH=y﹣(![]() ﹣2)2+4=
﹣2)2+4=![]() ,
,
∵BO∥CH,∴△ACH∽△ABC,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴OB=2,
,∴OB=2,
∴B(0,2);
(3)设点C的坐标为(x,﹣x2+4x),则H(x,0),
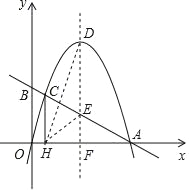
∵EF∥CH,∴△ACH∽△AEF,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴EF=2x,∴E(2,2x),
,∴EF=2x,∴E(2,2x),
∵EH=DE,∴![]() =4﹣2x,
=4﹣2x,
∴x1=﹣6+4![]() ,x2=﹣6﹣4
,x2=﹣6﹣4![]() (舍),
(舍),
∴EF=2x=﹣12+8![]() ,
,
∴E(2,﹣12+8![]() ).
).


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】问题情填,
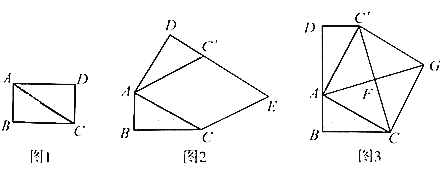
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动,如图1,将矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD、并且量得AB=2cm,AC=4cm.
操作发现:
(1)将图1中的△ACD以点A为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到加图2所示的△AC′D,过点C作AC′的平行线,与DC′的延长线交于点E,则四边形ACEC'的形状是_________;
(2)创新小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B,A,D三点在同一条直线上,得到如图3所示的△AC′D,连接CC′,取CC'的中点F,连精AF并延长到点G,使FG=AF,连接CG,C′G,得到四边形ACGC′,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至A′点,A′C与BC′相交于点H.如图4所示,连接CC',试求CH的长度.
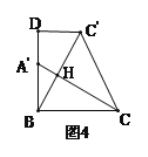
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A. C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y=![]() (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,
(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,![]() ).
).
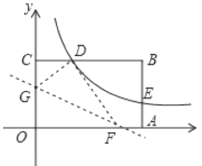
(1)求反比例函数的表达式和m的值;
(2)将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)甲、乙两家文具商店出售同样的毛笔和宣纸.毛笔每支18元,宣纸每张2元.甲商店推出的优惠方法为买一支毛笔送两张宣纸;乙商店的优惠方法为按总价的九折优惠.小丽想购买5支毛笔,宣纸x张(x≥5).
(1)若到甲商店购买,应付______ 元(用代数式表示);
(2)若到乙商店购买,应付______ 元(用代数式表示);
(3)若小丽要买宣纸10张,应选择哪家文具商店?若买100张呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
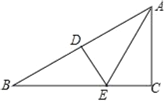
【题目】如图,在△ABC中,∠B=30°,边AB的垂直平分线分别交AB和BC于点D,E,且AE平分∠BAC.
(1)求∠C的度数;
(2)若CE=1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,CE=2.
(1)求AB的长;
(2)求⊙O的半径.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923086297137152/1923946164551680/STEM/edc8c851f08548f08f9e61b4dab2d43e.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB⊥AC,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转一个角度α(0°<α≤90°),分别交线段BC,AD于点E,F,连接BF.
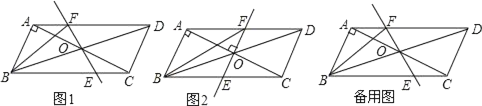
(1)如图1,在旋转的过程中,求证:OE=OF;
(2)如图2,当旋转至90°时,判断四边形ABEF的形状,并证明你的结论;
(3)若AB=1,BC=![]() ,且BF=DF,求旋转角度α的大小.
,且BF=DF,求旋转角度α的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
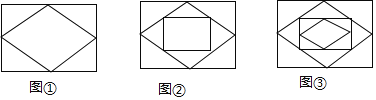
【题目】已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形.如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第3个图形中直角三角形的个数有______个,第2018个图形中直角三角形的个数有______个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com