
【题目】如图,在ABCD中,AB⊥AC,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转一个角度α(0°<α≤90°),分别交线段BC,AD于点E,F,连接BF.
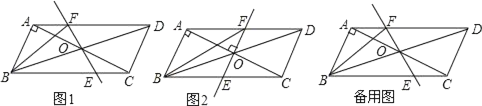
(1)如图1,在旋转的过程中,求证:OE=OF;
(2)如图2,当旋转至90°时,判断四边形ABEF的形状,并证明你的结论;
(3)若AB=1,BC=![]() ,且BF=DF,求旋转角度α的大小.
,且BF=DF,求旋转角度α的大小.
【答案】(1)证明见解析;(2)平行四边形,理由见解析;(3)45°
【解析】
(1)由平行四边形的性质得出∠OAF=∠OCE,OA=OC,进而判断出△AOF≌△COE,即可得出结论;
(2)先判断出∠BAC=∠AOF,得出AB∥EF,即可得出结论;
(3)先求出AC=2,进而得出A=1=AB,即可判断出△ABO是等腰直角三角形,进一步判断出△BFD是等腰三角形,利用等腰三角形的三线合一得出∠BOF=90°,即可得出结论.
(1)证明:在ABCD中,AD∥BC,
∴∠OAF=∠OCE,
∵OA=OC,∠AOF=∠COE,
∴△AOF≌△COE(ASA),
∴OE=OF;
(2)当旋转角为90°时,四边形ABEF是平行四边形,理由:
∵AB⊥AC,
∴∠BAC=90°,
∵∠AOF=90°,
∴∠BAC=∠AOF,
∴AB∥EF,
∵AF∥BE,
∴四边形ABEF是平行四边形;
(3)在Rt△ABC中,AB=1,BC=![]() ,
,
∴AC=![]() =2,
=2,
∴OA=1=AB,
∴△ABO是等腰直角三角形,
∴∠AOB=45°,
∵BF=DF,
∴△BFD是等腰三角形,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OF⊥BD(等腰三角形底边上的中线是底边上的高),
∴∠BOF=90°,
∴∠α=∠AOF=∠BOF﹣∠AOB=45°.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下来往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟后妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法中错误的是( )

A. 打电话时,小刚和妈妈的距离为1250米
B. 打完电话后,经过23分钟小刚到达学校
C. 小刚和妈妈相遇后,妈妈回家的速度为150米/分
D. 小刚家与学校的距离为2550米
查看答案和解析>>
科目:初中数学 来源: 题型:
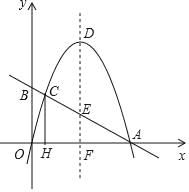
【题目】如图,二次函数y=﹣x2+bx的图象与x轴的正半轴交于点A(4,0),过A点的直线与y轴的正半轴交于点B,与二次函数的图象交于另一点C,过点C作CH⊥x轴,垂足为H.设二次函数图象的顶点为D,其对称轴与直线AB及x轴分别交于点E和点F.
(1)求这个二次函数的解析式;
(2)如果CE=3BC,求点B的坐标;
(3)如果△DHE是以DH为底边的等腰三角形,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足![]() +
+![]() =0,请回答问题:
=0,请回答问题:
(1)请直接写出a、b、c的值;
(2)数轴上a、b、c所对应的点分别为A、B、C,点M是A、B之间的一个动点,其对应的数为m,请化简![]() (请写出化简过程);
(请写出化简过程);
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动.若点A以每秒1个单位长度的速度向左运动.同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解并解答:
(1)我们把多项式![]() 及
及![]() 叫做完全平方式,在运用完全平方公式进行因式分解时,关键是判断这个多项式是不是一个完全平方式.同样地,把一个多项式进行部分因式分解可以来解决求代数式值的最大(或最小)值问题.
叫做完全平方式,在运用完全平方公式进行因式分解时,关键是判断这个多项式是不是一个完全平方式.同样地,把一个多项式进行部分因式分解可以来解决求代数式值的最大(或最小)值问题.
例如:①![]()
∵![]() 是非负数,即
是非负数,即![]() ≥0
≥0
∴![]() +2≥2
+2≥2
则这个代数式![]() 的最小值是_______,这时相应的
的最小值是_______,这时相应的![]() 的值是_______.
的值是_______.
②![]()
=![]()
=![]()
=![]()
=![]()
∵![]() 是非负数,即
是非负数,即![]() ≥0
≥0
∴![]() -7≥-7
-7≥-7
则这个代数式![]() 的最小值是____,这时相应的
的最小值是____,这时相应的![]() 的值是______.
的值是______.
(2)仿照上述方法求代数式 ![]() 的最大(或最小)值,并写出相应的
的最大(或最小)值,并写出相应的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是反比例函数![]() 的图象上的一个动点,连接OA,若将线段OA绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为________.
的图象上的一个动点,连接OA,若将线段OA绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
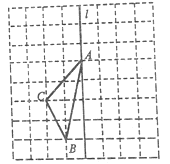
【题目】如图,由边长均为1个单位的小正方形组成的网格图中,点![]() 都在格点上。
都在格点上。
(1)![]() 的面积为__________________________;
的面积为__________________________;
(2)以![]() 为边画出一个与
为边画出一个与![]() 全等的三角形,并进一步探究:满足条件的三角形可以作出_____;
全等的三角形,并进一步探究:满足条件的三角形可以作出_____;
(3)在直线![]() 上确定点
上确定点![]() ,使
,使![]() 的长度最短.(画出示意图,并标明点
的长度最短.(画出示意图,并标明点![]() 的位置即可)
的位置即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m-3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
查看答案和解析>>
科目:初中数学 来源: 题型:
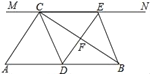
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com