
【题目】某经销商从市场得知如下信息:
A品牌计算器 | B品牌计算器 | |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他计划用不超过4万元的资金一次性购进这两种品牌计算器共100台,设该经销商购进A品牌计算器x台,这两种品牌计算器全部销售完后获得利润为y元.
(1)求y与x之间的函数关系式;
(2)若要求全部销售完后获得的利润不少于1.26万元,该经销商有哪几种进货方案?
(3)选择哪种进货方案,该经销商可获利最大?最大利润是多少元?
【答案】(1) ![]() ;(2) 三种进货方案,详见解析;(3)选择方案③进货时,经销商可获利最大,最大利润是13000元
;(2) 三种进货方案,详见解析;(3)选择方案③进货时,经销商可获利最大,最大利润是13000元
【解析】
(1)根据总利润=单块利润×购进数量,即可得出y关于x的函数关系式;
(2)根据总价=单价×购进数量结合(1)的结论,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,取其整数值即可得出各进货方案;
(3)由(1)的结论,利用一次函数的性质即可解决最值问题.
解:(1) ![]()
![]() ,
,
其中![]() ,得
,得![]() ,
,
即![]() ;
;
(2)令![]() ,则
,则![]() ,
,
![]() ,
,
又![]() ,
,
![]() .
.
![]() 为整数
为整数
![]() 经销商有以下三种进货方案:
经销商有以下三种进货方案:
方案 |
|
|
① | 48 | 52 |
② | 49 | 51 |
③ | 50 | 50 |
(3) ![]() ,
,
![]() 随
随![]() 的增大而增大,
的增大而增大,
![]() 时,
时,![]() 取得最大值,
取得最大值,
又![]() ,
,
![]() 选择方案③进货时,经销商可获利最大,最大利润是13000元。
选择方案③进货时,经销商可获利最大,最大利润是13000元。


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
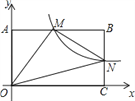
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=–![]() x+3交AB,BC于点M,N,反比例函数
x+3交AB,BC于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A. C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y=![]() (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,
(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,![]() ).
).
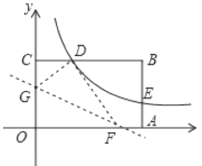
(1)求反比例函数的表达式和m的值;
(2)将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式。
查看答案和解析>>
科目:初中数学 来源: 题型:
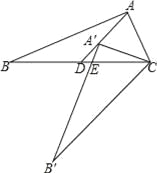
【题目】如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)甲、乙两家文具商店出售同样的毛笔和宣纸.毛笔每支18元,宣纸每张2元.甲商店推出的优惠方法为买一支毛笔送两张宣纸;乙商店的优惠方法为按总价的九折优惠.小丽想购买5支毛笔,宣纸x张(x≥5).
(1)若到甲商店购买,应付______ 元(用代数式表示);
(2)若到乙商店购买,应付______ 元(用代数式表示);
(3)若小丽要买宣纸10张,应选择哪家文具商店?若买100张呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,CE=2.
(1)求AB的长;
(2)求⊙O的半径.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923086297137152/1923946164551680/STEM/edc8c851f08548f08f9e61b4dab2d43e.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com