
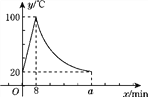
【题目】教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10 ℃,待加热到100 ℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20 ℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40 ℃的开水,则他需要在什么时间段内接水?
【答案】(1)当0≤x≤8时,y=10x+20;当8<x≤a时,y=![]() ;(2)a=40;(3)要想喝到不低于40℃的开水,x需满足8≤x≤20,即李老师要在7:38到7:50之间接水.
;(2)a=40;(3)要想喝到不低于40℃的开水,x需满足8≤x≤20,即李老师要在7:38到7:50之间接水.
【解析】试题分析:(1)当0≤x≤8时,设y=k1x+b,将(0,20),(8,100)的坐标分别代入y=k1x+b,即可求得k1、b的值,从而得一次函数的解析式;当8<x≤a时,设y=![]() ,将(8,100)的坐标代入y=
,将(8,100)的坐标代入y=![]() ,求得k2的值,即可得反比例函数的解析式;(2)把y=20代入反比例函数的解析式,即可求得a值;(3)把y=40代入反比例函数的解析式,求得对应x的值,根据想喝到不低于40 ℃的开水,结合函数图象求得x的取值范围,从而求得李老师接水的时间范围.
,求得k2的值,即可得反比例函数的解析式;(2)把y=20代入反比例函数的解析式,即可求得a值;(3)把y=40代入反比例函数的解析式,求得对应x的值,根据想喝到不低于40 ℃的开水,结合函数图象求得x的取值范围,从而求得李老师接水的时间范围.
试题解析:
(1)当0≤x≤8时,设y=k1x+b,
将(0,20),(8,100)的坐标分别代入y=k1x+b,可求得k1=10,b=20.
∴当0≤x≤8时,y=10x+20.
当8<x≤a时,设y=![]() ,
,
将(8,100)的坐标代入y=![]() ,
,
得k2=800.
∴当8<x≤a时,y=![]() .
.
综上,当0≤x≤8时,y=10x+20;
当8<x≤a时,y=![]() .
.
(2)将y=20代入y=![]() ,
,
解得x=40,即a=40.
(3)当y=40时,x=![]() =20.
=20.
∴要想喝到不低于40 ℃的开水,x需满足8≤x≤20,即李老师要在7:38到7:50之间接水.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=3,AB=9,过点A,C作相距为3的平行线段AE,CF,分别交CD,AB于点E,F,则FE的长是( ) 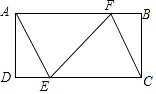
A.5
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于P(m,n),若点Q的坐标为(m,|m-n|),则称点Q为点P的关联点.
(1)请直接写出点(2,2)的关联点;
(2)如果点P在一次函数y=x-1的图像上,其“关联点”Q与点P重合,求点P的坐标;
(3)已知点P在一次函数y=x(x>0)和一次函数y=![]() x(x>0)所围成的区域内,且点P的“关联点”Q在二次函数
x(x>0)所围成的区域内,且点P的“关联点”Q在二次函数![]() 的图像上,求线段PQ的最大值及此时点P的坐标.
的图像上,求线段PQ的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系XOY中,有A(3,2),B (﹣1,﹣4 ),P是X轴上的一点,Q是Y轴上的一点,若以点A,B,P,Q四个点为顶点的四边形是平行四边形,则Q点的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为直线AB上一点,∠COE为直角,OF平分∠AOE.
(1)如图1,若∠COF=34°,则∠BOE=______;若∠COF=m°,则∠BOE=_______,∠BOE和∠COF的数量关系为_____________.
(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE和∠COF的数量关系是否还成立?请说明理由.
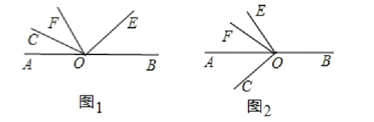
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com