
【题目】在平面直角坐标系xOy中,对于P(m,n),若点Q的坐标为(m,|m-n|),则称点Q为点P的关联点.
(1)请直接写出点(2,2)的关联点;
(2)如果点P在一次函数y=x-1的图像上,其“关联点”Q与点P重合,求点P的坐标;
(3)已知点P在一次函数y=x(x>0)和一次函数y=![]() x(x>0)所围成的区域内,且点P的“关联点”Q在二次函数
x(x>0)所围成的区域内,且点P的“关联点”Q在二次函数![]() 的图像上,求线段PQ的最大值及此时点P的坐标.
的图像上,求线段PQ的最大值及此时点P的坐标.
【答案】(1)(2;0);(2)(2;1) ;(3)PQ的最大值为![]() ,此时P(
,此时P(![]() ,
,![]() )
)
【解析】试题分析:(1)直接根据关联点的定义可求得答案;(2)设P(x,x-1),由关联点的定义表示出Q点的坐标,由Q与P重合可求得P点的坐标;(3)设点P的坐标为(a,b),由题意可知:a>0,b>0且a>b,2b>a,然后得到点Q的坐标为(a,a-b),再列出PQ与a的函数关系式,最后利用配方法可求得PQ的最大值,以及点P的坐标.
试题解析:(1)点(2,2)的关联点的坐标为(2,|22|),即(2,0).
(2)设P(x,x1),则点P的关联点的坐标为(x,1).
∵点P的“关联点”Q与点P重合,
∴x1=1,解得x=2.
∴点P的坐标为(2,1).
(3)设点P的坐标为(a,b).
∵点P在一次函数y=x(x>0)和一次函数y=![]() x(x>0)所围成的区域内,
x(x>0)所围成的区域内,
∴a>0,b>0且a>b,2b>a.
∴点P的“关联点”Q的坐标为(a,ab).
∵点Q在二次函数y=x2的图象上,
∴ab=a2,整理得b=aa2.
∵PQ=b(ab)=2ba,
∴PQ=2(aa2)a=2a2+a=2(a![]() )2+
)2+![]() .
.
∴当a=![]() 时,PQ有最大值,最大值为
时,PQ有最大值,最大值为![]() .
.
把a=![]() 代入b=aa2得b=
代入b=aa2得b=![]() .
.
∴点P的坐标为(![]() ,
,![]() 6).
6).


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )

A.-4 B.4 C.-2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点A、B、C、D的坐标依次为(﹣1,0),(m,n),(﹣1,10),(﹣9,p),且p≤n.若以A、B、C、D四个点为顶点的四边形是菱形,则n的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
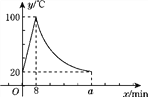
【题目】教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10 ℃,待加热到100 ℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20 ℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40 ℃的开水,则他需要在什么时间段内接水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种夹克和T恤,夹克每件定价100元,T恤每件定价60元,厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤 ②夹克和T恤都按定价的8折付款.
现某客户要到该服装厂购买夹克30件,T恤x件(x>30).
(1)若按方案①购买夹克和T恤共需 元(用含x的式子表示),若按方案②购买夹克和T恤共需 元(用含x的式子表示)
(2)若x=40,通过计算说明按方案①,②,哪种方案购买较为合算?
(3)当购买多少件T恤时,按以上两种方案购买所付价钱一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
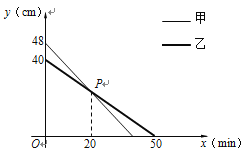
【题目】同时点燃甲乙两根蜡烛,蜡烛燃烧剩下的长度y(cm)与燃烧时间x(min)的关系如图所示.
(1)求乙蜡烛剩下的长度y与燃烧时间x的函数表达式;
(2)求点P的坐标,并说明其实际意义;
(3)求点燃多长时间,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com