
【题目】同时点燃甲乙两根蜡烛,蜡烛燃烧剩下的长度y(cm)与燃烧时间x(min)的关系如图所示.
(1)求乙蜡烛剩下的长度y与燃烧时间x的函数表达式;
(2)求点P的坐标,并说明其实际意义;
(3)求点燃多长时间,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍.
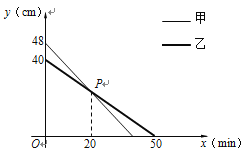
【答案】(1)y与x之间的函数表达式为y=-0.8x+40;
(2)点P的坐标为(20,24);点燃20分钟,甲乙两根蜡烛剩下的长度都是24 cm
(3)点燃12.5分钟,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍
【解析】试题分析:(1)根据直线经过点的坐标列方程组解答即可;
(2) 两直线的交点就是高度相同的时刻;
(3) 根据已知条件建立等式-1.2x+48=1.1(-0.8x+40),即可求出甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍.
试题解析:(1)设y与x之间的函数表达式为y=kx+b.
根据题意,当x=0时,y=40;当x=50时,y=0.
所以![]() ,解得
,解得![]() .
.
所以,y与x之间的函数表达式为y=-0.8x+40.
(2) P(20,24) 点燃20分钟,甲乙两根蜡烛剩下的长度都是24 cm.
(3)设甲蜡烛剩下的长度y甲与x之间的函数表达式为y甲=mx+n.
根据题意,当x=0时,y甲=48;当x=20时,y甲=24,
所以![]() ,解得
,解得![]() .
.
所以,y甲与x之间的函数表达式为y甲=-1.2x+48.
因为甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍,
所以 -1.2x+48=1.1(-0.8x+40)
解得 x=12.5
答:点燃12.5分钟,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为 . 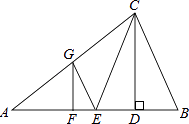
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于P(m,n),若点Q的坐标为(m,|m-n|),则称点Q为点P的关联点.
(1)请直接写出点(2,2)的关联点;
(2)如果点P在一次函数y=x-1的图像上,其“关联点”Q与点P重合,求点P的坐标;
(3)已知点P在一次函数y=x(x>0)和一次函数y=![]() x(x>0)所围成的区域内,且点P的“关联点”Q在二次函数
x(x>0)所围成的区域内,且点P的“关联点”Q在二次函数![]() 的图像上,求线段PQ的最大值及此时点P的坐标.
的图像上,求线段PQ的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人沿同一路线登山,图中线段OC、折线OAB分别是甲、乙两人登山的路程y(米)与登山时间x(分)之间的函数图象.请根据图象所提供的信息,解答如下问题:
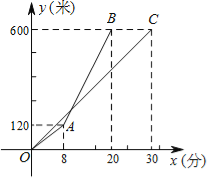
(1)求甲登山的路程与登山时间之间的函数关系式,并写出自变量x的取值范围;
(2)求乙出发后多长时间追上甲?此时乙所走的路程是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
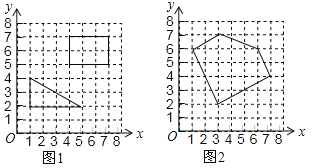
【题目】“皮克定理”是用来计算顶点在整点的多边形面积的公式,公式表达式为![]() ,孔明只记得公式中的S表示多边形的面积,a和b中有一个表示多边形边上(含顶点)的整点个数,另一个表示多边形内部的整点个数,但不记得究竟是a还是b表示多边形内部的整点个数,请你选择一些特殊的多边形(如图1)进行验证,得到公式中表示多边形内部的整点个数的字母是______,并运用这个公式求得图2中多边形的面积是____________.
,孔明只记得公式中的S表示多边形的面积,a和b中有一个表示多边形边上(含顶点)的整点个数,另一个表示多边形内部的整点个数,但不记得究竟是a还是b表示多边形内部的整点个数,请你选择一些特殊的多边形(如图1)进行验证,得到公式中表示多边形内部的整点个数的字母是______,并运用这个公式求得图2中多边形的面积是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[ ![]() ]=1,现对72进行如下操作:72
]=1,现对72进行如下操作:72 ![]() [
[ ![]() ]=8
]=8 ![]() [
[ ![]() ]=2
]=2 ![]() [
[ ![]() ]=1,这样对72只需进行3次操作即可变为1,类似地,对81只需进行次操作后即可变为1;(2)只需进行3次操作后变为2的所有正整数中,最大的是 .
]=1,这样对72只需进行3次操作即可变为1,类似地,对81只需进行次操作后即可变为1;(2)只需进行3次操作后变为2的所有正整数中,最大的是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com