【题目】解方程或方程组：
（1）
； （2）
；
（3）
【答案】（1）
；（2）
；（3）
【解析】试题分析：（1）按照去括号，移项，合并同类项，系数化为1的步骤解答即可；
（2）先两边乘以12去掉分母，然后按照去括号，移项，合并同类项，系数化为1的步骤解答即可；
（3）把②变形为y＝2x－5，然后代入①转化为一元一次方程，求出一元一次方程的解后，再代入③求出y的值即可．
试题解析：
解：（1）2(2x＋1)－(3x－4)＝2，
去括号得：4x＋2－3x＋4＝2，
移项并合并得：x＝－4；
（2）去分母得：3(3x－1)－2(5x－7)＝12，
去括号得：9x－3－10x＋14＝12，
移项并合并得：－x＝1，
系数化为1得：x＝－1；
（3）
，
由②得：y＝2x－5 ③，
把③代入①得：3x＋4(2x－5)＝2，
解得x＝2，
把x＝2代入③得：y＝－1，
所以原方程组的解为
．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
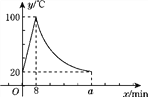
【题目】教师办公室有一种可以自动加热的饮水机，该饮水机的工作程序是：放满水后，接通电源，则自动开始加热，每分钟水温上升10 ℃，待加热到100 ℃，饮水机自动停止加热，水温开始下降，水温y(℃)和通电时间x(min)成反比例函数关系，直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温均为20 ℃，接通电源后，水温y(℃)和通电时间x(min)之间的关系如图所示，回答下列问题：
(1)分别求出当0≤x≤8和8＜x≤a时，y和x之间的函数关系式；
(2)求出图中a的值；
(3)李老师这天早上7：30将饮水机电源打开，若他想在8：10上课前喝到不低于40 ℃的开水，则他需要在什么时间段内接水？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某服装厂生产一种夹克和T恤，夹克每件定价100元，T恤每件定价60元，厂方在开展促销活动期间，向客户提供两种优惠方案：①买一件夹克送一件T恤 ②夹克和T恤都按定价的8折付款．
现某客户要到该服装厂购买夹克30件，T恤x件（x＞30）．
（1）若按方案①购买夹克和T恤共需 元（用含x的式子表示），若按方案②购买夹克和T恤共需 元（用含x的式子表示）
（2）若x=40，通过计算说明按方案①，②，哪种方案购买较为合算？
（3）当购买多少件T恤时，按以上两种方案购买所付价钱一样多？
查看答案和解析>>
科目：初中数学 来源： 题型：
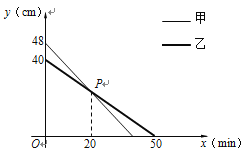
【题目】同时点燃甲乙两根蜡烛，蜡烛燃烧剩下的长度y（cm）与燃烧时间x（min）的关系如图所示．
（1）求乙蜡烛剩下的长度y与燃烧时间x的函数表达式；
（2）求点P的坐标，并说明其实际意义；
（3）求点燃多长时间，甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=6，AC=8，则BC边上中线AD的取值范围为（ ） （提示：可以构造平行四边形）
A.2＜AD＜14
B.1＜AD＜7
C.6＜AD＜8
D.12＜AD＜16
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从地面到高空11千米之间，气温随高度的升高而下降，每升高1千米，气温下降6℃.已知某处地面气温为23℃，设该处离地面 x千米（0＜x＜11）从的温度为y℃，则y与x的函数关系式为_________________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：
若x满足(x－2015)(2002－x)=－302，试求(x－2015)2＋(2002－x)2的值．
解：设x－2015=a,2002－x=b，则ab=－302且a＋b=(x－2015)＋(2002－x)=－13.
∵(a＋b)2=a2＋2ab＋b2，
∴a2＋b2=(a＋b)2－2ab=(－13)2－2×(－302)=773，即(x－2015)2＋(2002－x)2的值为773.
解决问题：
请你根据上述材料的解题思路，完成下面一题的解答过程，若y满足(y－2015)2＋(y－2016)2=4035，试求(y－2015)(y－2016)的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
