
【题目】已知O为直线AB上一点,∠COE为直角,OF平分∠AOE.
(1)如图1,若∠COF=34°,则∠BOE=______;若∠COF=m°,则∠BOE=_______,∠BOE和∠COF的数量关系为_____________.
(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE和∠COF的数量关系是否还成立?请说明理由.
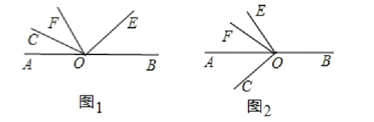
【答案】(1)68°;2m°;∠BOE=2∠COF;(2)∠BOE=2∠COF成立.
【解析】试题分析:(1)已知∠COE是直角,∠COF=34°,即可求得∠EOF=56°,再由OF平分∠AOE,可得∠AOE =112°,根据平角的定义求得∠BOE=68°;当∠COF=m°,可得∠EOF=90°-m°,所以∠AOE=2∠EOF=180°-2m°,根据平角的定义可得∠BOE=2m°,从而得∠BOE=2∠COF.(2)∠BOE和∠COF的数量关系仍然成立,类比(1)的方法即可解决.
试题解析:
(1)∵∠COE是直角,∠COF=34°,
∴∠EOF=90°-34°=56°,
由∵OF平分∠AOE.
∴∠AOE=2∠EOF=112°,
∴∠BOE=180°-112°=68°;
当∠COF=m°,
∴∠EOF=90°-m°,
∴∠AOE=2∠EOF=180°-2m°,
∴∠BOE=180°-(180°-2m°)=2m°,
所以有∠BOE=2∠COF.
故答案为68°;2m°;∠BOE=2∠COF;
(2)∠BOE和∠COF的数量关系仍然成立,
∵∠COE是直角
∴∠EOF=90°-∠COF
又∵OF平分∠AOE
∴∠AOE=2∠EOF
∴∠BOE=180°-∠AOE=180°-2(90°-∠COF)=2∠COF.


科目:初中数学 来源: 题型:
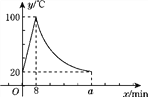
【题目】教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10 ℃,待加热到100 ℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20 ℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40 ℃的开水,则他需要在什么时间段内接水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=6,AC=8,则BC边上中线AD的取值范围为( ) (提示:可以构造平行四边形)
A.2<AD<14
B.1<AD<7
C.6<AD<8
D.12<AD<16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从地面到高空11千米之间,气温随高度的升高而下降,每升高1千米,气温下降6℃.已知某处地面气温为23℃,设该处离地面 x千米(0<x<11)从的温度为y℃,则y与x的函数关系式为_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出第二组的频率是0.08,乙同学计算出从左至右第一、二、三、四组的频数比为2:4:17:15.结合统计图回答下列问题:
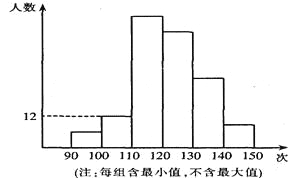
(1)这次共抽调了多少人?
(2)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是多少?
(3)若该校九年级有600名学生,请估计该校九年级达到优秀的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
若x满足(x-2015)(2002-x)=-302,试求(x-2015)2+(2002-x)2的值.
解:设x-2015=a,2002-x=b,则ab=-302且a+b=(x-2015)+(2002-x)=-13.
∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2-2ab=(-13)2-2×(-302)=773,即(x-2015)2+(2002-x)2的值为773.
解决问题:
请你根据上述材料的解题思路,完成下面一题的解答过程,若y满足(y-2015)2+(y-2016)2=4035,试求(y-2015)(y-2016)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com