
【题目】如图、四边形ABCD中,AB=AD=6,∠A=60°,∠ADC=150°,已知四边形的周长为30,求四边形ABCD的面积. 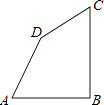
【答案】解:连接BD,作DE⊥AB于E, 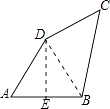
∵AB=AD=6,∠A=60°,
∴△ABD是等边三角形,
∴AE=BE= ![]() AB=3,
AB=3,
∴DE= ![]() =3
=3 ![]() ,
,
因而△ABD的面积是= ![]() ×ABDE=
×ABDE= ![]() ×6×3
×6×3 ![]() =9
=9 ![]() ,
,
∵∠ADC=150°
∴∠CDB=150°﹣60°=90°,
则△BCD是直角三角形,
又∵四边形的周长为30,
∴CD+BC=30﹣AD﹣AB=30﹣6﹣6=18,
设CD=x,则BC=18﹣x,
根据勾股定理得到62+x2=(18﹣x)2
解得x=8,
∴△BCD的面积是 ![]() ×6×8=24,
×6×8=24,
S四边形ABCD=S△ABD+S△BDC=9 ![]() +24.
+24.
答:四边形ABCD的面积是9 ![]() +24.
+24.
【解析】连接BD,易证△ABD是等边三角形,△BCD是直角三角形,因而只要求出CD与BD的长就可以求出结果.
【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):

(1)报名参加课外活动小组的学生共有 人,将条形图补充完整;
(2)扇形图中m= ,n= ;
(3)根据报名情况,学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组,甲、乙恰好都被安排到“地方戏曲”小组的概率是多少?请用列表或画树状图的方法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某校七(1)班学生的平均身高是160厘米,下表给出了该班6名学生的身高情况(单位:厘米).
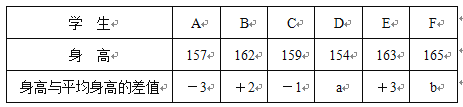
(1)列式计算表中的数据a和b;
(2)这6名学生中谁最高?谁最矮?最高与最矮学生的身高相差多少?
(3)这6名学生的平均身高与全班学生的平均身高相比,在数值上有什么关系?(通过计算回答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )

A.-4 B.4 C.-2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y2(x2)21是由y2x2怎样平移得到的( )
A.先向左平移2个单位长度,再向上平移1个单位长度
B.先向左平移2个单位长度,再向下平移1个单位长度
C.先向右平移2个单位长度,再向上平移1个单位长度
D.先向右平移2个单位长度,再向下平移1个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
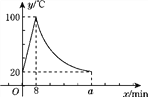
【题目】教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10 ℃,待加热到100 ℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20 ℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40 ℃的开水,则他需要在什么时间段内接水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=6,AC=8,则BC边上中线AD的取值范围为( ) (提示:可以构造平行四边形)
A.2<AD<14
B.1<AD<7
C.6<AD<8
D.12<AD<16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com