
【题目】如图,矩形ABCD中,AD=3,AB=9,过点A,C作相距为3的平行线段AE,CF,分别交CD,AB于点E,F,则FE的长是( ) 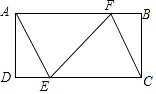
A.5
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:过F作FH⊥AE于H,如图所示: 则FH=3=AD,
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∵AE∥CF,
∴四边形AECF是平行四边形,
∴AF=CE,
∴DE=BF,
∴AF=9﹣DE,
∴AE= ![]() ,
,
∵∠FHA=∠D=∠DAF=90°,
∴∠AFH+∠HAF=∠DAE+∠FAH=90°,
∴∠DAE=∠AFH,
∴△ADE∽△AFH,
∴ ![]() =
= ![]() =1,
=1,
∴AE=AF,DE=AH,
∴ ![]() =9﹣DE,
=9﹣DE,
解得:DE=4,
∴AH=4,
∴AF=AE= ![]() =5,
=5,
∴HE=AE﹣AH=1,
∴EF= ![]() =
= ![]() =
= ![]() ;
;
故选:C.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2
(1)是一元二次方程;
(2)是一元一次方程;
(3)若x=﹣2是它的一个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )

A.-4 B.4 C.-2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y2(x2)21是由y2x2怎样平移得到的( )
A.先向左平移2个单位长度,再向上平移1个单位长度
B.先向左平移2个单位长度,再向下平移1个单位长度
C.先向右平移2个单位长度,再向上平移1个单位长度
D.先向右平移2个单位长度,再向下平移1个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点A、B、C、D的坐标依次为(﹣1,0),(m,n),(﹣1,10),(﹣9,p),且p≤n.若以A、B、C、D四个点为顶点的四边形是菱形,则n的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
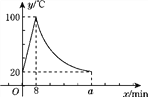
【题目】教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10 ℃,待加热到100 ℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20 ℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40 ℃的开水,则他需要在什么时间段内接水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种夹克和T恤,夹克每件定价100元,T恤每件定价60元,厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤 ②夹克和T恤都按定价的8折付款.
现某客户要到该服装厂购买夹克30件,T恤x件(x>30).
(1)若按方案①购买夹克和T恤共需 元(用含x的式子表示),若按方案②购买夹克和T恤共需 元(用含x的式子表示)
(2)若x=40,通过计算说明按方案①,②,哪种方案购买较为合算?
(3)当购买多少件T恤时,按以上两种方案购买所付价钱一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从地面到高空11千米之间,气温随高度的升高而下降,每升高1千米,气温下降6℃.已知某处地面气温为23℃,设该处离地面 x千米(0<x<11)从的温度为y℃,则y与x的函数关系式为_________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com