
 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F.分析 (1)只要证明∠DBF=∠DAC,即可判断.
(2)利用相似三角形的性质即可解决问题.
解答 (1)证明:如图,∵AD⊥BC,BE⊥AC
∴∠BDF=∠ADC=∠BEC=90°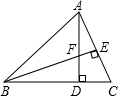
∴∠C+∠DBF=90°,∠C+∠DAC=90°
∴∠DBF=∠DAC
∴△ACD∽△BFD;
(2)解:如图,∵∠ABD=45°,∠ADB=90°,
∴AD=BD,
∴$\frac{AD}{BD}$=1,
∵△ACD∽△BFD,AC=3,
∴$\frac{AC}{BF}=\frac{AD}{BD}$=1,
∴BF=AC=3.
点评 本题考查相似三角形的性质和判定,同角的余角相等,直角三角形两锐角互余等知识,解题的关键是正确寻找相似三角形,利用新三角形的性质解决问题,属于中考常考题型.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com