一个不透明的袋中装有3个小球,分别标有数字-2、3、-4,这些小球除所有标数字不同外,其余完全相同,小明从中任意摸出一球,所标数字记为x,另有4张背面完全相同,正面分别标有数字3、-1、-4、5的卡片,小亮将其混合后,背面超上放置于桌面,并从中随机抽取一张,卡片上的数字记为y.
(1)若以x为横坐标,y为纵坐标,求点A(x,y)落在第二象限的概率(要求用列表法或树状图求解)
(2)小明和小亮做游戏,规则是若点A(x,y)落在第二象限,则小明赢:若A(x,y)落在第三象限,则小亮赢,你认为这个游戏公平吗?请说明理由.
分析:(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果.
(2)游戏是否公平,求出游戏双方获胜的概率,比较是否相等即可.
解答:解:(1)列树状图如下
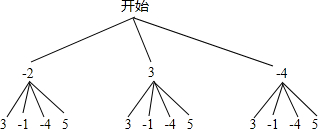
,
共有12种等可能的结果,符合条件的情况有4种,
所以P(点A落在第二象限)=
=
.
(2)公平.理由如下,由(1)得P(点A落在第三象限)=
=
.
P(点A落在第二象限)=P(点A落在第三象限).
所以游戏公平.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.
