Question

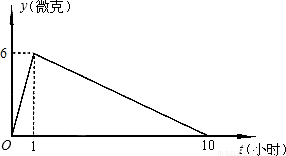
在全国抗击“非典”的斗争中，黄冈研究所的医学专家们经过日夜奋战，终于研制出一种治疗非典型肺炎的抗生素．据临床观察：如果成人按规定的剂量注射这种抗生素，注射药液后每毫升血液中的含药量y(微克)与时间t(时)之间的函数关系近似地满足图中所示的折线．

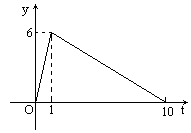
(1)写出注射药液后每毫升血液中含药量y与时间t之间的函数关系式及自变量的取值范围．

(2)根据临床观察：每毫升血液中含药量不少于4微克时，控制“非典”病情是有效的．如果病人按规定的剂量注射该药液后，经过多长时间开始有效控制病情？这个有效时间有多长？

(3)假若某病人一天中第一次注射药液是早晨6点钟，问怎样安排此人从6∶00～20∶00注射药液的时间，才能使病人的治疗效果最好？

Answer 1

答案：
解析：

解　　(1)当0≤t≤1时，设 　　y＝k1t， 　　则　　6＝k1×1，k1＝6 　　所以　　y＝6t 　　当1≤t≤10时，设 　　y＝k2t＋b， 　　则　　 　　解得　　 　　所以　　y＝－t＋ 　　所以所求函数关系式为 　　y＝ 　　(2)当0≤t≤1时，令y＝4，得6t＝4，所以 　　t＝ 　　(或6t≥4，所以t≥) 　　当1≤t≤10时，令y＝4，得－t＋＝4，所以 　　t＝4． 　　(或－t＋≥4，所以t≤4．) 　　所以注射药液小时后开始有效，有效时间长为： 　　4－＝(时)． 　　(3)设第二次注射药液的时间是在第一次注射药液后t1小时， 　　则　　－t1＋＝4， 　　解得　　t1＝4(时) 　　所以第二次注射药液的时间是10∶00． 　　设第三次注射药液的时间是在第一次注射药液后t2小时，此时体内的含药量是第一次注射药液的含药量与第二次注射的含药量之和，则 　　－t2＋－(t2－4)＋＝4， 　　解得　　t2＝9(时) 　　所以第三次注射药液的时间是15∶00． 　　设第四次的注射药液时间是在第一次注射液后t3小时，此时体内不再含第一次注射药液的药量(因为t3＞10)，体内的含药量是第二次注射液的含药量与第三次注射药液的含药量之和，则 　　－(t3－4)＋－(t3－9)＋＝4， 　　解得　　t3＝13(时) 　　所以第四次注射药液的时间是19∶30． 　　所以安排此人注射药液的时间为：第一次注射药液的时间是6∶00，第二次注射药液的时间是10∶00，第三次注射药液的时间是15∶00，第四次注射药液的时间是19∶30，这样安排才使病人的治疗效果最好．