
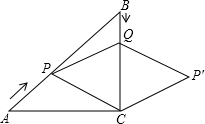
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒
如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒| 2 |
| 2 |
| ||
| 2 |
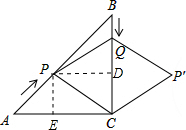 解:作PD⊥BC于D,PE⊥AC于E,如图,AP=
解:作PD⊥BC于D,PE⊥AC于E,如图,AP=| 2 |
| ||
| 2 |


科目:初中数学 来源: 题型:
 Ⅰ.解不等式组5-x<2x-1≤9,并把解集在数轴上表示出来.
Ⅰ.解不等式组5-x<2x-1≤9,并把解集在数轴上表示出来.| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、了解炮弹的杀伤力,采用普查的方式 |
| B、了解全国中学生的睡眠状况,采用普查的方式 |
| C、了解人们保护水资源的意识,采用抽样调查的方式 |
| D、对载人航天器“神舟六号”零部件的检查,采用抽样调查的方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知A(-2,n)B(3,-2)是一次函数y=kx+b的图象和反比例函数y=
如图,已知A(-2,n)B(3,-2)是一次函数y=kx+b的图象和反比例函数y=| m |
| x |
| m |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com