
����Ŀ����5�ı���������ÿ���Ӫ�˹������£���x������100Ԫʱ���۹��ȫ���������x����100Ԫʱ��ÿ�����������ÿ����5Ԫ�����ȥ�Ĺ۹�ͻ����1������֪���й۹ÿ��Ĺ�������1100Ԫ��
��1���Żݻ�ڼ䣬Ϊʹ�۹ȫ�������ÿ��ľ�����Ϊ������ÿ���������������ӦΪ����Ԫ����ע��������=����멁�����ѣ�
��2����ÿ�����������Ϊ����Ԫʱ��ÿ��ľ�������ࣿ
���𰸡���1��ÿ���������������ӦΪ25Ԫ����2����ÿ�����������Ϊ175Ԫʱ��ÿ��ľ����������5025Ԫ��
��������
�����������1���۹ȫ�����ÿ��ľ�����=�������г��������멁�����ѣ���������Ϊ���г�����ʽ��⼴�ɣ���2���ɺ�������ʽ�Ƿֶκ�������ÿһ��������������ֵ���Ƚϵó����������ֵ��
�����������1��������֪�����۹��ȫ���������0��x��100��
��50x��1100��0��
���x��22��
�֡�x��5�ı�����
��ÿ���������������ӦΪ25Ԫ��
��2����ÿ�����ľ�����ΪyԪ��
��0��x��100ʱ��y1=50x��1100��
��y1��x�����������
�൱x=100ʱ��y1�����ֵΪ50��100��1100=3900��
��x��100ʱ��
y2=��50��![]() ��x��1100
��x��1100
=��![]() x2+70x��1100
x2+70x��1100
=��![]() ��x��175��2+5025��
��x��175��2+5025��
��x=175ʱ��y2�����ֵΪ5025��
5025��3900��
�ʵ�ÿ�����������Ϊ175Ԫʱ��ÿ��ľ����������5025Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����:7,12,11,10,13,8,7,14,9,10,8,11,10,8,10,9,12,9,13,11,�����������ڷ�Χ8.5��11.5�ڵ�Ƶ��Ӧ����(����)
A. 8 B. 9 C. 10 D. 11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MON=90�㣬��A��B�ֱ�������OM��ON���˶���BEƽ�֡�NBA��BE�ķ����ӳ������BAO��ƽ���߽��ڵ�C�����C�Ķ����ǣ� �� 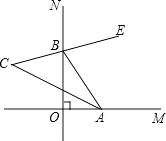
A.30��
B.45��
C.55��
D.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ABC=��ACB����A=40�㣬P�ǡ�ABC��һ�㣬�ҡ�ACP=��PBC�����BPC= �� 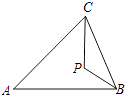
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��һԪ���η���4x2-4x+c=0���������ʵ��������c��ֵ�ǣ�������.
A.-1
B.1
C.-4
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�ķ���x2+2x+a=0������ʵ��������a��ȡֵ��Χ�ǣ�������.
A.a��1
B.a��1
C.a��1
D.a��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������2013����˾�����Ϊ30000Ԫ��2015���˾�����Ϊ36300Ԫ����2013�굽2015���˾��������ƽ����������ͬ�����˾��������������ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com