
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=( ) 
A.![]()
B.![]()
C.![]()
D.![]() ﹣2
﹣2
【答案】A
【解析】解:∵AB=AD=6,AM:MB=AN:ND=1:2, ∴AM=AN=2,BM=DN=4,
连接MN,连接AC,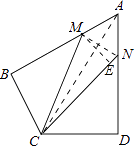
∵AB⊥BC,AD⊥CD,∠BAD=60°
在Rt△ABC与Rt△ADC中,![]() ,
,
∴Rt△ABC≌Rt△ADC(HL)
∴∠BAC=∠DAC= ![]() ∠BAD=30°,MC=NC,
∠BAD=30°,MC=NC,
∴BC= ![]() AC,
AC,
∴AC2=BC2+AB2 , 即(2BC)2=BC2+AB2 ,
3BC2=AB2 ,
∴BC=2 ![]() ,
,
在Rt△BMC中,CM= ![]() =
= ![]() =2
=2 ![]() .
.
∵AN=AM,∠MAN=60°,
∴△MAN是等边三角形,
∴MN=AM=AN=2,
过M点作ME⊥CN于E,设NE=x,则CE=2 ![]() ﹣x,
﹣x,
∴MN2﹣NE2=MC2﹣EC2 , 即4﹣x2=(2 ![]() )2﹣(2
)2﹣(2 ![]() ﹣x)2 ,
﹣x)2 ,
解得:x= ![]() ,
,
∴EC=2 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴ME= ![]() =
= ![]() ,
,
∴tan∠MCN= ![]() =
= ![]()
故选:A.
连接AC,通过三角形全等,求得∠BAC=30°,从而求得BC的长,然后根据勾股定理求得CM的长,连接MN,过M点作ME⊥CN于E,则△MNA是等边三角形求得MN=2,设NE=x,表示出CE,根据勾股定理即可求得ME,然后求得tan∠MCN.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过(﹣1,m2+2m+1)、(0,m2+2m+2)两点,其中m为常数.
(1)求b的值,并用含m的代数式表示c;
(2)若抛物线y=x2+bx+c与x轴有公共点,求m的值;
(3)设(a,y1)、(a+2,y2)是抛物线y=x2+bx+c上的两点,请比较y2﹣y1与0的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从甲地匀速驶往乙地,到达后用了半小时卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍.货车离甲地的距离y(千米)关于时间x(小时)的函数图象如图所示.则a=(小时). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明从点A处出发,沿着坡角为α的斜坡向上走了0.65千米到达点B,sinα= ![]() ,然后又沿着坡度为i=1:4的斜坡向上走了1千米达到点C.问小明从A点到点C上升的高度CD是多少千米(结果保留根号)?
,然后又沿着坡度为i=1:4的斜坡向上走了1千米达到点C.问小明从A点到点C上升的高度CD是多少千米(结果保留根号)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分2 , 则成绩较为整齐的是队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数y= ![]() 图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).
图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).
(1)k=;
(2)试说明AE=BF;
(3)当四边形ABCD的面积为 ![]() 时,求点P的坐标.
时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB为等腰三角形,顶点A的坐标(2, ![]() ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,4
,4 ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com