
【题目】如图,小明从点A处出发,沿着坡角为α的斜坡向上走了0.65千米到达点B,sinα= ![]() ,然后又沿着坡度为i=1:4的斜坡向上走了1千米达到点C.问小明从A点到点C上升的高度CD是多少千米(结果保留根号)?
,然后又沿着坡度为i=1:4的斜坡向上走了1千米达到点C.问小明从A点到点C上升的高度CD是多少千米(结果保留根号)?
【答案】解:如图所示:过点B作BF⊥AD于点F,过点C作CD⊥AD于点D,
由题意得:AB=0.65千米,BC=1千米,
∴sinα= ![]() =
= ![]() ,
,
∴BF=0.65× ![]() =0.25(km),
=0.25(km),
∵斜坡BC的坡度为:1:4,
∴CE:BE=1:4,
设CE=x,则BE=4x,
由勾股定理得:x2+(4x)2=12
解得:x= ![]() ,
,
∴CD=CE+DE=BF+CE= ![]() +
+ ![]() ,
,
答:点C相对于起点A升高了( ![]() +
+ ![]() )km.
)km.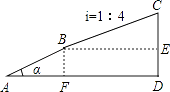
【解析】根据题意画出图形,进而利用锐角三角函数关系分别求出BF,CE的长,即可得出点C相对于起点A升高的高度.
【考点精析】通过灵活运用锐角三角函数的定义,掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数即可以解答此题.


科目:初中数学 来源: 题型:
【题目】李师傅加工1个甲种零件和1个乙种零件的时间分别是固定的,现知道李师傅加工3个甲种零件和5个乙种零件共需55分钟;加工4个甲种零件和9个乙种零件共需85分钟,则李师傅加工2个甲种零件和4个乙种零件共需分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,已知A(﹣1,0)、B(3,0)、C(0,﹣1)三点,D(1,m)是一个动点,当△ACD的周长最小时,△ABD的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ ![]() x+1的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′.
x+1的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′. 
(1)当α=60°时,判断点B是否在直线O′B′上,并说明理由;
(2)连接OO′,设OO′与AB交于点D,当α为何值时,四边形ADO′B′是平行四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=( ) 
A.![]()
B.![]()
C.![]()
D.![]() ﹣2
﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H. 
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,一块等腰直角三角板ABC的直角顶点A在y轴上,坐标为(0,﹣1),另一顶点B坐标为(﹣2,0),已知二次函数y= ![]() x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y轴且经过点B,直尺沿x轴正方向平移,当A′D′与y轴重合时运动停止.
(1)求点C的坐标及二次函数的关系式;
(2)若运动过程中直尺的边A′D′交边BC于点M,交抛物线于点N,求线段MN长度的最大值;
(3)如图②,设点P为直尺的边A′D′上的任一点,连接PA、PB、PC,Q为BC的中点,试探究:在直尺平移的过程中,当PQ= ![]() 时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
(说明:点与抛物线的位置关系可分为三类,例如,图②中,点A在抛物线内,点C在抛物线上,点D′在抛物线外.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、②分别是某种型号跑步机的实物图与示意图,已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m). (参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com