


| 1 | 2 |
|
| AC |
| BC |
| CD |
| CE |
| a |
| b |
| AD |
| BE |
| AC |
| BC |
| a |
| b |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 25 |
| 4 |
| 25 |
| 4 |
| 125 |
| 4 |


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
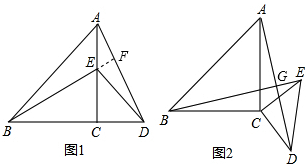
��ͼ1�� E�ǵ���Rt��ABC��AC�ϵ�һ������(��E��A��C���غ�)����CEΪһ����Rt��ABC������Rt��CDE������AD�� BE������̽������ͼ���߶�AD�����߶�BE �ij��ȹ�ϵ������ֱ�ߵ�λ�ù�ϵ��

��1���ٲ�����ͼ1���߶�BG���߶�DE�ij��ȹ�ϵ������ֱ�ߵ�λ�ù�ϵ���ڽ�ͼ1�еĵ���Rt��CDE���ŵ�C��˳ʱ�뷽����ת����Ƕ�![]() ���õ���ͼ2����ͼ3���Σ�����ͨ���۲졢�����ȷ����жϢ��еõ��Ľ����Ƿ���Ȼ����,��ѡȡͼ2֤������жϣ�
���õ���ͼ2����ͼ3���Σ�����ͨ���۲졢�����ȷ����жϢ��еõ��Ľ����Ƿ���Ȼ����,��ѡȡͼ2֤������жϣ�

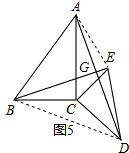
��2����ԭ���е���ֱ�������θ�Ϊֱ�������Σ���ͼ4��6������AC=a��BC=b��CD=ka�� CE=kb (a![]() b��k
b��k![]() 0)����(1)����еõ��Ľ�����Щ��������Щ������������������ͼ5Ϊ����Ҫ˵�����ɣ�
0)����(1)����еõ��Ľ�����Щ��������Щ������������������ͼ5Ϊ����Ҫ˵�����ɣ�
��3���ڵ�(2)��ͼ5�У�����BD��AE����a=4��b=3��k=![]() ����BD2+AE2��ֵ��
����BD2+AE2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

 ���õ���ͼ2����ͼ3���Σ�����ͨ���۲졢�����ȷ����жϢ��еõ��Ľ����Ƿ���Ȼ����,��ѡȡͼ2֤������жϣ�
���õ���ͼ2����ͼ3���Σ�����ͨ���۲졢�����ȷ����жϢ��еõ��Ľ����Ƿ���Ȼ����,��ѡȡͼ2֤������жϣ�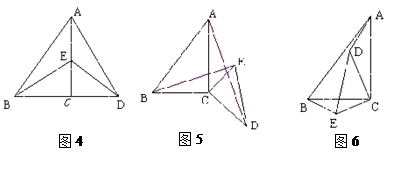
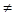 b��k
b��k 0)����(1)����еõ��Ľ�����Щ��������Щ������������������ͼ5Ϊ����Ҫ˵�����ɣ�
0)����(1)����еõ��Ľ�����Щ��������Щ������������������ͼ5Ϊ����Ҫ˵�����ɣ�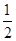 ����BD2+AE2��ֵ��
����BD2+AE2��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�콭��ʡ�γ��н��·ѧУ�п�������ѧ������������ ���ͣ������
��ͼ1�� E�ǵ���Rt��ABC��AC�ϵ�һ������(��E��A��C���غ�)����CEΪһ����Rt��ABC������Rt��CDE������AD�� BE������̽������ͼ���߶�AD�����߶�BE �ij��ȹ�ϵ������ֱ�ߵ�λ�ù�ϵ�� 
��1���ٲ�����ͼ1���߶�BG���߶�DE�ij��ȹ�ϵ������ֱ�ߵ�λ�ù�ϵ���ڽ�ͼ1�еĵ���Rt��CDE���ŵ�C��˳ʱ�뷽����ת����Ƕ� ���õ���ͼ2����ͼ3���Σ�����ͨ���۲졢�����ȷ����жϢ��еõ��Ľ����Ƿ���Ȼ����,��ѡȡͼ2֤������жϣ�
���õ���ͼ2����ͼ3���Σ�����ͨ���۲졢�����ȷ����жϢ��еõ��Ľ����Ƿ���Ȼ����,��ѡȡͼ2֤������жϣ�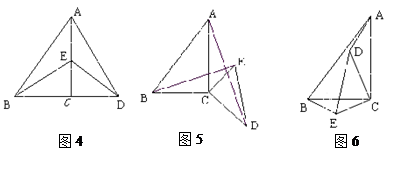
��2����ԭ���е���ֱ�������θ�Ϊֱ�������Σ���ͼ4��6������AC=a��BC=b��CD=ka�� CE="kb" (a b��k
b��k 0)����(1)����еõ��Ľ�����Щ��������Щ������������������ͼ5Ϊ����Ҫ˵�����ɣ�
0)����(1)����еõ��Ľ�����Щ��������Щ������������������ͼ5Ϊ����Ҫ˵�����ɣ�
��3���ڵ�(2)��ͼ5�У�����BD��AE����a=4��b=3��k= ����BD2+AE2��ֵ��
����BD2+AE2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ�꽭��ʡ�γ��н��·ѧУ�п�������ѧ���������棩 ���ͣ������
��ͼ1�� E�ǵ���Rt��ABC��AC�ϵ�һ������(��E��A��C���غ�)����CEΪһ����Rt��ABC������Rt��CDE������AD�� BE������̽������ͼ���߶�AD�����߶�BE �ij��ȹ�ϵ������ֱ�ߵ�λ�ù�ϵ��

��1���ٲ�����ͼ1���߶�BG���߶�DE�ij��ȹ�ϵ������ֱ�ߵ�λ�ù�ϵ���ڽ�ͼ1�еĵ���Rt��CDE���ŵ�C��˳ʱ�뷽����ת����Ƕ� ���õ���ͼ2����ͼ3���Σ�����ͨ���۲졢�����ȷ����жϢ��еõ��Ľ����Ƿ���Ȼ����,��ѡȡͼ2֤������жϣ�
���õ���ͼ2����ͼ3���Σ�����ͨ���۲졢�����ȷ����жϢ��еõ��Ľ����Ƿ���Ȼ����,��ѡȡͼ2֤������жϣ�

��2����ԭ���е���ֱ�������θ�Ϊֱ�������Σ���ͼ4��6������AC=a��BC=b��CD=ka�� CE=kb (a b��k
b��k 0)����(1)����еõ��Ľ�����Щ��������Щ������������������ͼ5Ϊ����Ҫ˵�����ɣ�
0)����(1)����еõ��Ľ�����Щ��������Щ������������������ͼ5Ϊ����Ҫ˵�����ɣ�
��3���ڵ�(2)��ͼ5�У�����BD��AE����a=4��b=3��k= ����BD2+AE2��ֵ��
����BD2+AE2��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com