解:根据题意可得
abc<0,
a+b+c>0,
那么①a<0,b>0,c>0,
②a>0,b>0,c<0,
③a>0,b<0,c>0,
∴①当a<0,b>0,c>0时,x=
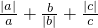
=-1+1+1=1,
∴2009x
2-2008x+2010=2009-2008+2010=2011;
②当a>0,b>0,c<0时,x=
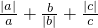
=1+1-1=1,
∴2009x
2-2008x+2010=2009-2008+2010=2011;
③当a>0,b<0,c>0时,x=
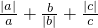
=1-1+1=1,
∴2009x
2-2008x+2010=2009-2008+2010=2011.
故2009x
2-2008x+2010的值是2011.
分析:首先,由题意可得abc<0,a+b+c>0,从而可知分3种情况:①a<0,b>0,c>0,②a>0,b>0,c<0,③a>0,b<0,c>0,分别计算每一种情况下x的值,再把x的值代入所求代数式计算即可.
点评:本题考查了代数式求值.解题的关键是根据已知条件得出a、b、c的取值范围.

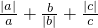 时,求2009x2-2008x+2010的值.
时,求2009x2-2008x+2010的值.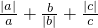 =-1+1+1=1,
=-1+1+1=1,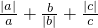 =1+1-1=1,
=1+1-1=1,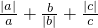 =1-1+1=1,
=1-1+1=1,
