解:(1)∵在△ABC中,∠ABC=60°,∠ACB=70°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC=

∠ABC=

×60°=30°,∠OCB=

∠ACB=

×70°=35°,
∴∠BOC=180°-∠OBC-∠OCB=180°-30°-35°=115°;
(2)∵在△ABC中,∠A=80°,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=

(∠ABC+∠ACB)=

(180°-80°)=50°,
∴∠BOC=180°-50°=130°;
(3)在△ABC中,∠A=k,BD和CE分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=

(∠ABC+∠ACB)=

(180°-k)=90°-

k,
∴∠BOC=180°-(90°-

k)=90°+

k.
分析:(1)先根据角平分线的性质得出∠OBC与∠OCB的度数,再根据三角形内角和定理即可得出结论;
(2)先根据∠A=80°求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠OBC+∠OCB的度数,根据三角形内角和定理即可得出结论;
(3)根据∠A=k求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠OBC+∠OCB的度数,根据三角形内角和定理即可得出结论.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键

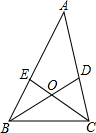 如图,在△ABC中,BD和CE分别平分∠ABC和∠ACB.
如图,在△ABC中,BD和CE分别平分∠ABC和∠ACB. ∠ABC=
∠ABC= ×60°=30°,∠OCB=
×60°=30°,∠OCB= ∠ACB=
∠ACB= ×70°=35°,
×70°=35°, (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (180°-80°)=50°,
(180°-80°)=50°, (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (180°-k)=90°-
(180°-k)=90°- k,
k, k)=90°+
k)=90°+ k.
k.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为