练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】把下列各数填入相应的集合中:

    -6, 9.3, -, 15, 0, -0.33, -0.333…, 1.41421356, -3, 3.3030030003…, -3.1415926.

    正数集合:{ … }

    负数集合: { … }

    有理数集合: { … }

    无理数集合: { … }

    【答案】见解析.

    【解析】

    根据大于零的数是正数，可得正数集合；根据小于零的数是负数，可得负数集合；根据有理数是有限小数或无限循环小数，可得有理数集合；根据无理数是无限不循环小数，可得无理数集合．

    正数集合:{ 9.3, 15, 1.41421356, 3.3030030003… … },

    负数集合: {-6, -, -0.33, -0.333…, -3, -3.1415926. … },

    有理数集合: {-6, 9.3, -, 15, 0, -0.33, -0.333…, 1.41421356, -3.1415926 … },

    无理数集合: { -3, 3.3030030003…, … }.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，要建一个长方形养鸡场，养鸡场的一边靠墙（墙长25米），另三边用竹篱笆围成，竹篱笆的长为40米，若要围成的养鸡场的面积为180平方米，求养鸡场的宽各为多少米，设与墙平行的一边长为x米．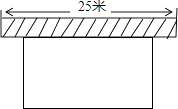
    （1）填空：（用含x的代数式表示）另一边长为米；
    （2）列出方程，并求出问题的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为∣AB∣.当A、B两点中有一点在原点时，不妨设点A在原点，如图1，∣AB∣＝∣OB∣＝∣b∣＝∣a-b∣；当A、B两点都不在原点时，如图2，点A、B都在原点的右边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣；如图3，点A、B都在原点的左边，∣AB∣＝∣OB∣－∣OA∣＝∣b∣-∣a∣=－b-（-a）=∣a-b∣；如图4，点A、B在原点的两边，∣AB∣＝∣OB∣+∣OA∣＝∣a∣+∣b∣=a+（-b）=∣a-b∣；

    回答下列问题：

    （1）数轴上表示2和5的两点之间的距离是　　　,数轴上表示－2和－5的两点之间的距离是　　　　,数轴上表示1和－3的两点之间的距离是　　　　.

    （2）数轴上表示x和－1的两点A和B之间的距离是　　　　,如果∣AB∣＝2，那么x为　　　　；

    （3）当代数式∣x+1∣+∣x-2∣取最小值时，相应的x的取值范围是　　　　.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①为一种平板电脑保护套的支架效果图，AM固定于平板电脑背面，与可活动的MB、CB部分组成支架．平板电脑的下端N保持在保护套CB上，不考虑拐角处的弧度及平板电脑和保护套的厚度，绘制成图②，其中AN表示平板电脑，M为AN上的定点，AN=CB=20cm，AM=8cm，MB=MN，我们把∠ANB叫做倾斜角，根据以上数据，判断倾斜角能小于30°吗？请说明理由．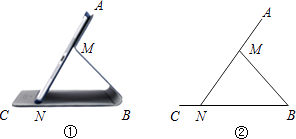

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示的运算程序中，若开始输入的x值为48，我们发现第一次输出的结果为24，第二次输出的结果为12，…，则第2018次输出的结果为________．

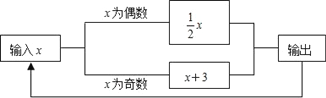
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为积极响应政府提出的“绿色发展·低碳出行”号召，某社区决定购置一批共享单车，经市场调查得知，购买3量男式单车与4辆女式单车费用相同，购买5辆男式单车与4辆女式单车共需16000元.

    (1)求男式单车和女式单车的单价；

    (2)该社区要求男式单比女式单车多4辆，两种单车至少需要22辆，购置两种单车的费用不超过50000元，该社区有几种购置方案？怎样购置才能使所需总费用最低，最低费用是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足 = ，连接AF并延长交⊙O于点E，连接AD，DE，若CF=2，AF=3，给出下列结论：①△ADF∽△AED；②FG=2；③tanE= ；④S△DEF=4 ，其中正确的是（ ）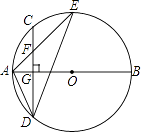
    A.①②③
    B.②③④
    C.①②④
    D.①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有三张正面分别标有数字：﹣1，1，2的卡片，它们除数字不同外其余全部相同，现将它们背面朝上，洗匀后从中抽出一张记下数字，放回洗匀后再从中随机抽出一张记下数字．
    （1）请用列表或画树形图的方法（只选其中一种），表示两次抽出卡片上的数字的所有结果；
    （2）将第一次抽出的数字作为点的横坐标x，第二次抽出的数字作为点的纵坐标y，求点（x，y）落在双曲线y= 上的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3．5万元，购买2台电脑和1台电子白板需要2．5万元．

    （1）求每台电脑、每台电子白板各多少万元？

    （2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低．

    查看答案和解析>>

    同步练习册答案