Question

如图1，A、E、F、C在一条直线上，AE=CF，∠1=∠2，∠3=∠4．
（1）试说明AB=CD的理由；
（2）连接BD，则BD平分EF；
（3）若将△DEC的边EC沿AC方向移动变为图2时，其余条件不变，上述（2）的结论是否成立？请直接回答，不需说明理由．

Answer 1

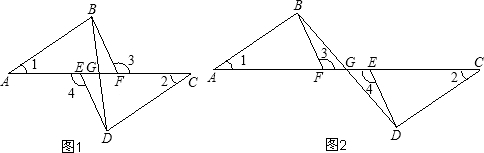
解：（1）∵∠3=∠4，
∴∠AFB=∠CED，
∵AE=CF，
∴AE+EF=CF+EF，
∴AF=CE，
又∵∠1=∠2，
∴△ABF≌△CDE，
∴AB=CD；

（2）∵△ABF≌△CDE，
∴BF=DE，
又∵∠3=∠4，
∴∠BFG=∠DEG，
又∵∠BGF=∠DGE，
∴△DEG≌△BFG，
∴EG=FG，
即BD平分EF．

（3）答：（2）中的结论仍然成立．
分析：（1）由于∠3=∠4，利用等角的补角相等，可得∠AFB=∠CED，而AE=CF，那么AE+EF=CF+EF，即AF=CE，再加上∠1=∠2，利用ASA可证△ABF≌△CDE，再利用全等三角形的性质，可得AB=CD；（2）由于（1）中△ABF≌△CDE，那么BF=DE，再由∠3=∠4，可得∠BFG=∠DEG，且∠BGF=∠DGE，利用AAS可证△DEG≌△BFG，再利用全等三角形的性质，可得EG=FG，即BD平分EF．
点评：本题考查了全等三角形的判定和性质；做题过程中多次用了全等三角形的判定，选择判定方法时要根据已知条件的位置，选择最简单的方法．